Предмет: Геометрия,
автор: Anna2105
Стороны треугольника равны a, b, c. Докажите, что медиана, проведённая к стороне c, равна .
Приложения:
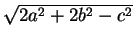
Ответы
Автор ответа:
2
Надо "достроить" треугольник до параллелограмма, продлив медиану на "свою" длину за сторону с и соединив полученную точку с концами с.
Три вершины А В С, четвертая вершина полученного параллелограмма пусть Е.
Если обозначить x = cos(угол АСВ), то соs(угол САЕ) = cos(180 - угол АСВ) = -x.
По теореме косинусов для тр-ка АВС
c^2 = a^2 + b^2 - 2*a*b*x;
По теореме косинусов для тр-ка САЕ со сторонами b, a, 2*m (m - медиана тр-ка АВС к стороне с)
(2*m)^2 = a^2 + b^2 + 2*a*b*x;
Осталось сложить оба равенства.
(2*m)^2 = 2*(a^2 + b^2) - c^2;
Если поделить на 4, получится известная формула для длины медианы.
Похожие вопросы
Предмет: Другие предметы,
автор: 2610z
Предмет: Другие предметы,
автор: dnadosha
Предмет: Русский язык,
автор: Яношка
Предмет: Литература,
автор: ketalucta
Предмет: Химия,
автор: viktoria1885