докажите, что для любых трёх точек,не лежащих на одной прямой ,справедливы неравенства : AB<AC+CB,AC<AB+BC,BC<BA+AC
Ответы
Это просто утверждения о том, что длина стороны треугольника меньше суммы длин остальных сторон.
Наверно, можно придумать какое-то "доказательство", но это чаще всего принимают аксиомой.
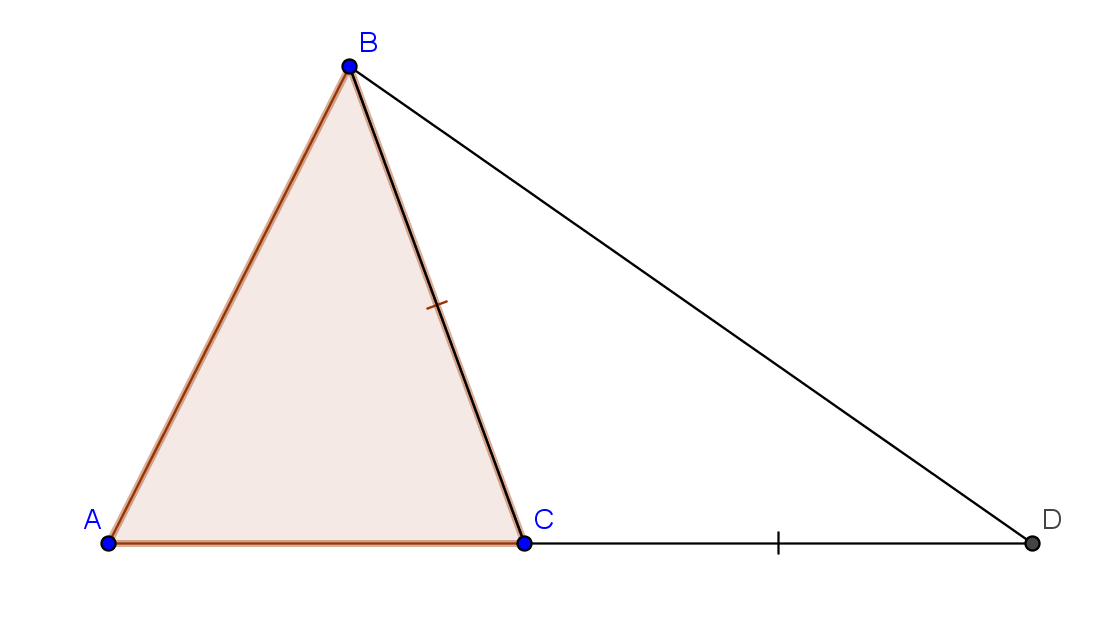
Хотя "доказательство" в курсе геометрии также приводится. Отложим на продолжении прямой АС отрезок СD=BC. Треугольник CDB - равнобедренный, поэтому у него равны углы при основании. Очевидно, угол D больше угла ABD (внутри последнего помещается угол, равный углу D). Т.к. против Ольшего угла лежит бОльшая сторона, то AD>AB. А т.к. AD=AC+CB, то неравенство доказано.
Несколько слов о том, почему "доказательство". Дело в том, что в школьной геометрии аккуратно (а иногда и не очень) обходится стороной вопрос о том, что же такое "длина". Можно говорить о том, что это "сколько раз один отрезочек помещается в другом". Но существуют несоизмеримые отрезки (т.е. длины этих отрезков не относятся друг к другу как целые числа). Почему в таком случае все-таки длина существует, строго говоря не очень понятно. Поэтому "длину" определяют с помощью набора аксиом, одной из которых обычно выбираю неравенство треугольника.