Question

Найдите высоту цилиндра наибольшего объема,который можно вписать в шар радиуса 2 корень из 3 м

Answer 1

Ответ: 4м.

Объяснение:

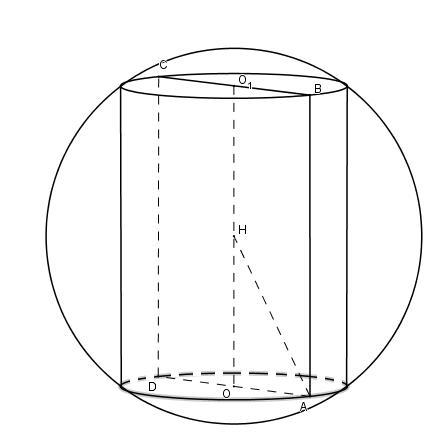
Шар можно описать около любого цилиндра. Окружности оснований цилиндра лежат на поверхности шара. Центр шара лежит на середине высоты, проходящей через ось цилиндра.

$\boldsymbol{O_1H=OH}$ . Из условия: AH = 2√3 м;

Пусть $\boldsymbol{OO_1}=x$ м, тогда $\boldsymbol{OH=\dfrac{x}{2}}$ м. Из прямоугольного треугольника AOH найдем AO

$\boldsymbol{AO=\sqrt{AH^2-OH^2}=\sqrt{12^2-\left(\dfrac{x}{2}\right)^2}=\dfrac{1}{2}\sqrt{48-x^2}}$

$\boldsymbol{48-x^2\geq0~~and~~~~x\geq0~~\Longleftrightarrow~~~ 0\leq x\leq 4\sqrt{3}}$

Рассмотрим функцию: $\boldsymbol{V(x)=\dfrac{1}{3}S_oh=\dfrac{1}{3}\cdot \pi\cdot \left(\dfrac{1}{2}\sqrt{48-x^2}\right)^2\cdot x=\dfrac{\pi}{12}\left(48x-x^3\right)}$

$\boldsymbol{V'(x)=\dfrac{\pi}{12}\left(48-3x^2\right)=\dfrac{\pi}{4}\left(16-x^2\right)=0}\\ \\ \boldsymbol{x=\pm4}$

[0]_____+____[4]____-____[4√3]

x = 4 - относительный максимум, значит искомая высота $\boldsymbol{OO_1=4}$ м