Question

Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны 2*корень из двух и 4, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

1) площадь боковой поверхности параллелепипеда;

2) площадь полной поверхности параллелепипеда.

3) объем параллелепипеда.

Answer 1

Дано: a=2√2, b=4 α=45, h=h(меньш.пар.)

Найти: S(б), S, V

Решение:

1)Найдем боковую площадь параллепипеда.

Для этого нам нужно узнать его высоту, а она равна меньшей высоте параллелограмма.

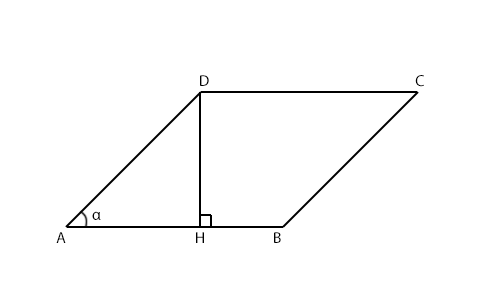
Рисуем параллелограм, который лежит в основании и проводим эту меньшую высоту (во вложениях фото)

Я обозначил эту меньшую высоту как DH. Очевидно, если DH меньшая высота, то DA=2√2, DC=4

Найдем DH

$<var>DH=DA*sin\alpha=2\sqrt2*\frac{\sqrt2}{2}=2</var>$

нашли меньшую высоту параллелограмма, а значит и нашли высоту паллелепипеда

h=DH=2

Так как

DA=BC, AB=DC

площадь боковой поверхности можно записать так

$<var>S_b=(2AB+2BC)*h=2h*(AB+BC)=\\ =2*2(4+2\sqrt2)=8(2+\sqrt2)=16+8\sqrt2</var>$

 

2)Полная повехность параллелепипеда складывается из двух площадей основания и боковой поверхности.

$<var>S=2S_{osn}+S_b</var>$

Найдем площадь основания, формула достатоно легкая

$<var>S_{osn}=a*b*sin\alpha=AB*DA*sin45=4*2\sqrt2*\frac{\sqrt2}{2}=8</var>$

$<var>S=2S_{osn}+S=2*8+16+8\sqrt2=32+8\sqrt2</var>$

 

3)Ну а зная площадь основания и восоту, которые мы уже нашли до этого, объем найти легко:

$<var>V=S_{osn}*h=8*2=16</var>$

 

Ответ:

1)16+8√2

2)32+8√2

3)16