Предмет: Геометрия,
автор: mariel24012003
помогите срооооочно
диагонали прямоугольника abcd пересекаются в точке о. отрезок ct биссектриса треугольника acd. точки p,e середины отрезков at, ct соответственно. вычислите периметр четырёхугольника poet если угол bac=60 градусов и td=6 см
Ответы
Автор ответа:
0
1)
Угол ВАС = углу АСД (накрест лежащие при ВС пар-но АД и секущей АС)
Углы АСТ и ТСД равны(по условию)
Они по 30 градусов
Рассмотрим треугольник СТД.
Угол С = 30 градусов, угол Д = 90 градусов
А катет, лежащий против угла 30 градусов равен половине гипотенузы
СТ = 6*2 = 12
По теореме пифагора
СД =корень квадратный из 144-38 =к.к. из 108 = 6 корней из 3
А периметр равен:
18*2 + 6 √3 * 2 =36 + 12√3
Если есть ответы, сверься, потому что то, что Р и Е середины я не использовала, и зачем дана точка О тоже не понятно. Условие точно правильное, потому что у треугольнико АСД не может быть бис-сы, а вот у угла АСД - вполне
Угол ВАС = углу АСД (накрест лежащие при ВС пар-но АД и секущей АС)
Углы АСТ и ТСД равны(по условию)
Они по 30 градусов
Рассмотрим треугольник СТД.
Угол С = 30 градусов, угол Д = 90 градусов
А катет, лежащий против угла 30 градусов равен половине гипотенузы
СТ = 6*2 = 12
По теореме пифагора
СД =корень квадратный из 144-38 =к.к. из 108 = 6 корней из 3
А периметр равен:
18*2 + 6 √3 * 2 =36 + 12√3
Если есть ответы, сверься, потому что то, что Р и Е середины я не использовала, и зачем дана точка О тоже не понятно. Условие точно правильное, потому что у треугольнико АСД не может быть бис-сы, а вот у угла АСД - вполне
Автор ответа:
0
пропустила некоторые моменты, если интересно - посмотри моё решение, оно вроде больше похоже на правильное и используются все данные
Автор ответа:
0
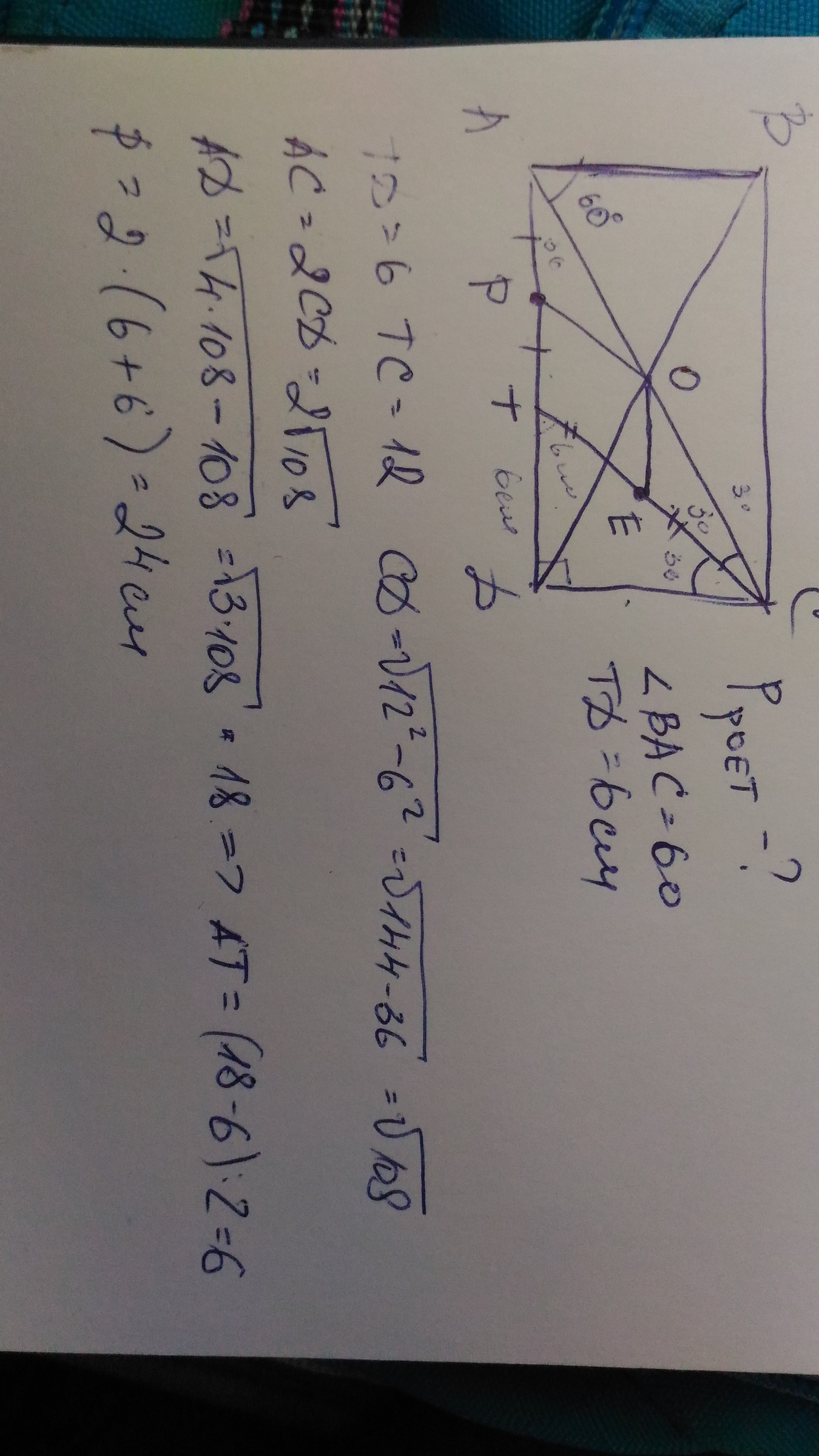
1. Угол АСD=60 как накрест лежащий, следовательно углы ACT=TCD=30.
2. Треугольник CTD прямоугольный, и катет, лежащий против угла в 30 градусов равен половине гипотенузы, следовательно СТ=12 см и ТЕ=6.
3. Тр-к CTD. По теореме Пифагора найдём CD.
4. Треугольник АСD. Угол CAD=30 и следовательно СD=½АС.
См. фото.
Р=24
2. Треугольник CTD прямоугольный, и катет, лежащий против угла в 30 градусов равен половине гипотенузы, следовательно СТ=12 см и ТЕ=6.
3. Тр-к CTD. По теореме Пифагора найдём CD.
4. Треугольник АСD. Угол CAD=30 и следовательно СD=½АС.
См. фото.
Р=24
Приложения:
Автор ответа:
0
Ага, поняла. У меня Р оказалась серединой АД, а не АТ)
Похожие вопросы
Предмет: Информатика,
автор: kusakinilya
Предмет: Математика,
автор: kemranuharanov
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: Аноним