Предмет: Геометрия,
автор: Аноним
Биссектрисы углов A и B параллелограмма ABCD делят сторону CD на три отрезка!Найдите длину каждого отрезка,если стороны параллелограмма равны 5 см и 12 см+нарисуйте рисунок.Помогите пожалуйста,буду признательня
Ответы
Автор ответа:
0
Биссектриса параллелограмма отсекает от него равнобедренный треугольник. Это свойство основано на равенстве накрестлежащих углов при пересечении параллельных прямых (стороны параллелограмма) секущей ( биссектриса)
Пусть биссектриса угла А будет АМ, угла В - ВК.
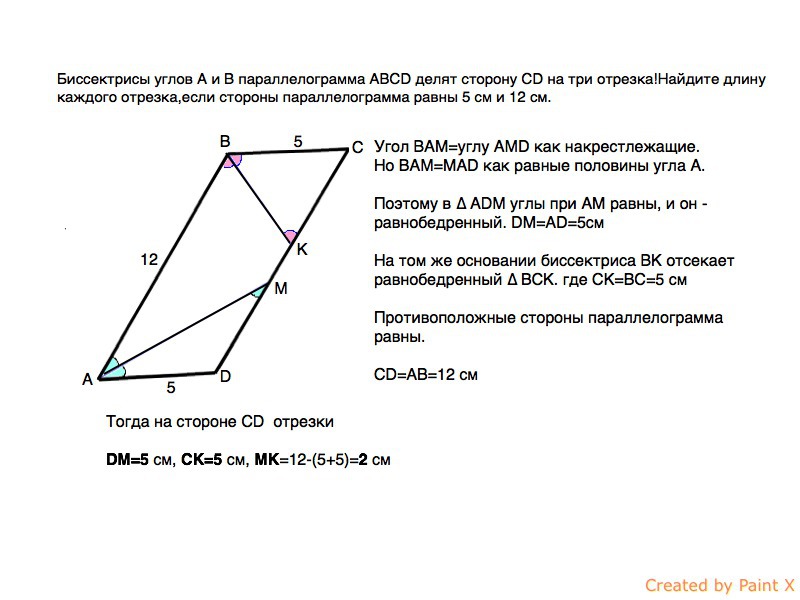
Угол ВАМ=углу АМD как накрестлежащие, Но ВАМ=МАD как равные половины угла А. Поэтому в ∆ АDM углы при АМ равны, и он - равнобедренный. DM=AD=5см
На том же основании ВК отсекает равнобедренный ∆ ВСК. где СК=ВС=5 см
СD=AB=12 см
Тогда на стороне CD отрезки
DМ=5 см, СК=5 см, МК=12-(5+5)=2 см
Пусть биссектриса угла А будет АМ, угла В - ВК.
Угол ВАМ=углу АМD как накрестлежащие, Но ВАМ=МАD как равные половины угла А. Поэтому в ∆ АDM углы при АМ равны, и он - равнобедренный. DM=AD=5см
На том же основании ВК отсекает равнобедренный ∆ ВСК. где СК=ВС=5 см
СD=AB=12 см
Тогда на стороне CD отрезки
DМ=5 см, СК=5 см, МК=12-(5+5)=2 см
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: История,
автор: katialebedinec
Предмет: Математика,
автор: marianamedoncak
Предмет: Математика,
автор: Iepik36
Предмет: Математика,
автор: ramazansilash