Предмет: Геометрия,
автор: nastya1594
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отно- шении AP:PB=CQ:QB=CW:WD=1: 4 , радиус окружности, описанной около треугольника PQW, равен 10, PQ= 16, QW =12 . а) Докажите, что треугольник PQW — прямоугольный. б) Найдите площадь четырёхугольника ABCD .
Ответы
Автор ответа:
0
Треугольник PQW не обязательно прямоугольный. По т. синусов для него получаем PW=2R·sin∠Q=20·sin∠Q, а по т. косинусов для него же
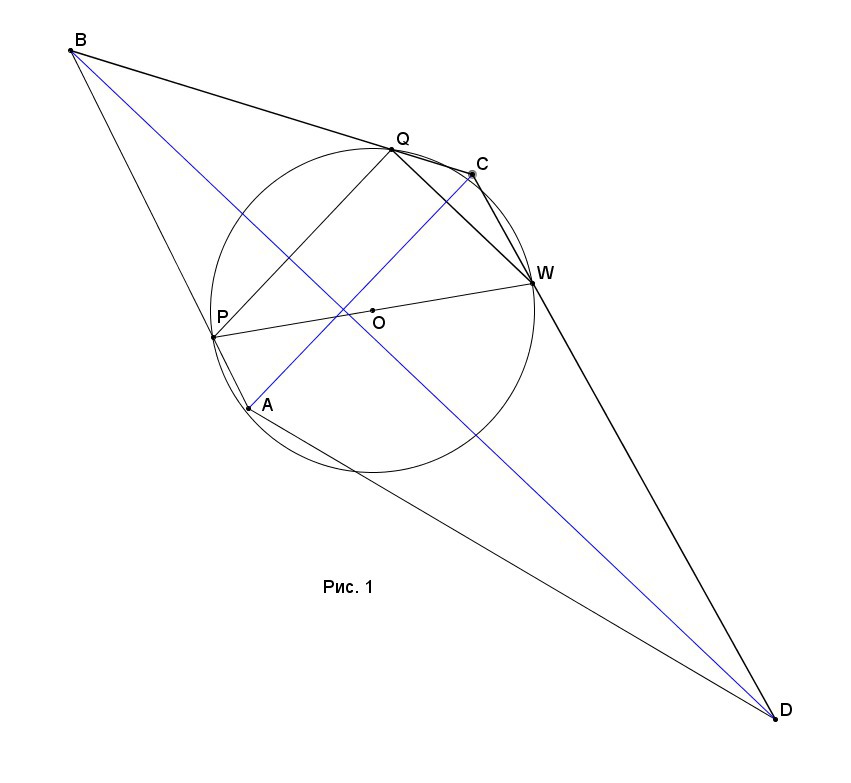
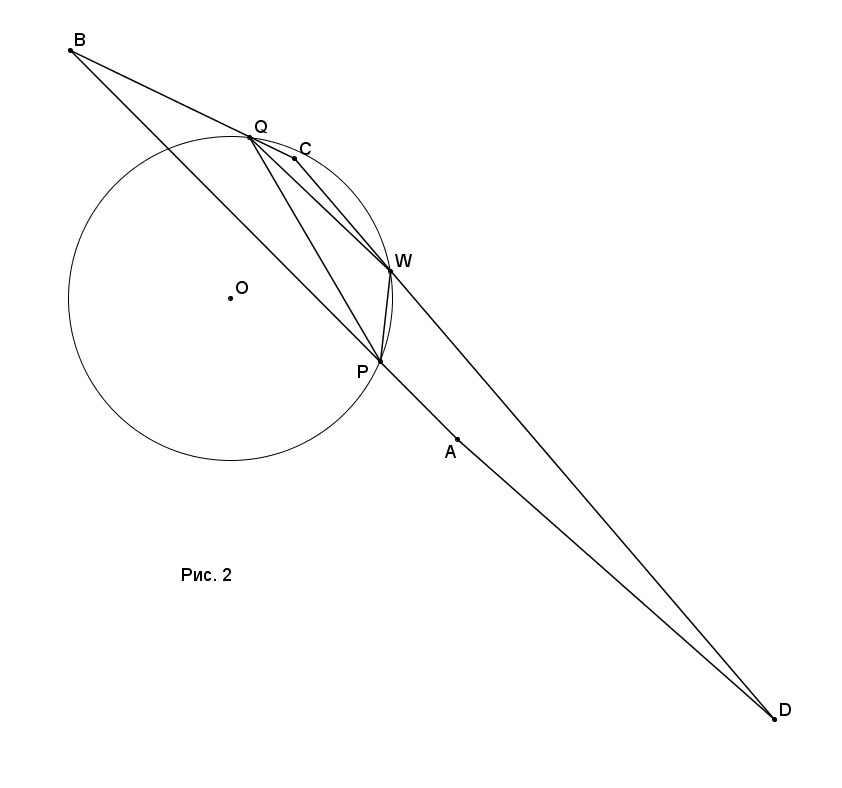
20²·sin²∠Q=16²+12²-2·16·12·cos∠Q. Решаем это уравнение, получаем cos∠Q=0 и cos∠Q=24/25. Т.е. в первом случае PQW - действительно прямоугольный (см. рис. 1), а второй случай также существует при выпуклом ABCD (см. рис. 2.)
Т.к. AB/PB=CB/QB=5/4, то треугольник ABC подобен треугольнику PBQ с коэффициентом подобия 5/4, откуда AC=(5/4)·PQ=5*16/4=20 и AC||PQ. Аналогично, треугольник BCD подобен треугольнику QCW с коэффициентом 5, т.е. BD=5QW=5*12=60 и BD||QW, откуда угол между диагоналями ABCD равен углу PQW. Площадь ABCD вычисляется по формуле (1/2)AC·BD·sin(∠PQW).
Значит, в случае, когда PQW - прямоугольный
S(ABCD)=(1/2)·20·60·sin(90°)=600.
Во втором случае
S(ABCD)=(1/2)·20·60·√(1-24²/25²)=168.
20²·sin²∠Q=16²+12²-2·16·12·cos∠Q. Решаем это уравнение, получаем cos∠Q=0 и cos∠Q=24/25. Т.е. в первом случае PQW - действительно прямоугольный (см. рис. 1), а второй случай также существует при выпуклом ABCD (см. рис. 2.)
Т.к. AB/PB=CB/QB=5/4, то треугольник ABC подобен треугольнику PBQ с коэффициентом подобия 5/4, откуда AC=(5/4)·PQ=5*16/4=20 и AC||PQ. Аналогично, треугольник BCD подобен треугольнику QCW с коэффициентом 5, т.е. BD=5QW=5*12=60 и BD||QW, откуда угол между диагоналями ABCD равен углу PQW. Площадь ABCD вычисляется по формуле (1/2)AC·BD·sin(∠PQW).
Значит, в случае, когда PQW - прямоугольный
S(ABCD)=(1/2)·20·60·sin(90°)=600.
Во втором случае
S(ABCD)=(1/2)·20·60·√(1-24²/25²)=168.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sofiechka999
Предмет: Алгебра,
автор: dievening
Предмет: Математика,
автор: kolz200763
Предмет: Литература,
автор: bondarvalentin