Question

В параллелограмме ABCD,из вершины B тупого угла ABC проведен перпендикуляр BK к стороне AD(K принадлежит AD) и BK=0,5 Найдите углы параллелограмма

Answer 1

Полное условие задания:

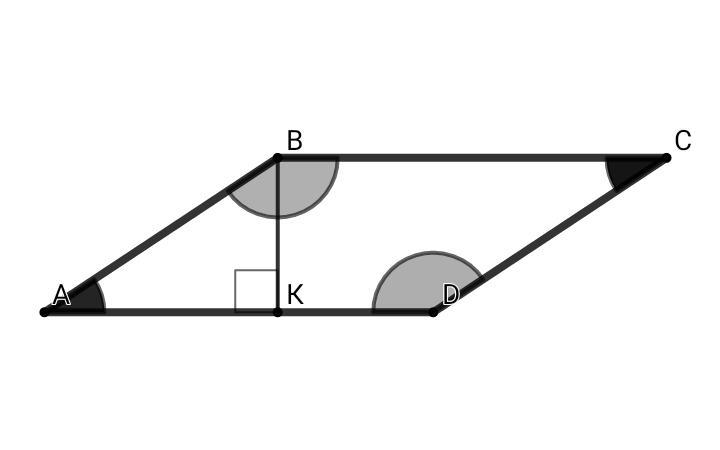
В параллелограмме ABCD, из вершины тупого угла В Δ ABC проведен перпендикуляр BK к стороне AD (K ∈ AD) и BK = 0,5•AB. Найдите углы параллелограмма.

• Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны, а углы попарно равны

ВК = АВ/2

В прямоугольном ΔАВК: катет ВК, лежащий против ∠ А, равен половине гипотенузы АВ   ⇒  ∠А = 30°

∠ABC + ∠BAD = 180° - как односторонние углы при BC || AD и секущей АВ  ⇒ ∠ABC = 180° - ∠BAD = 180° - 30° = 150°

∠А = ∠С = 30° , ∠B = ∠D = 150°

Ответ: 30° , 150° , 30° , 150°