Предмет: Алгебра,
автор: алина199
Помогите пожалуйста,срочно!
Упростите:
Приложения:

Ответы
Автор ответа:
0
Решение во вложении
Постаралась расписать достаточно подробно
Приложения:
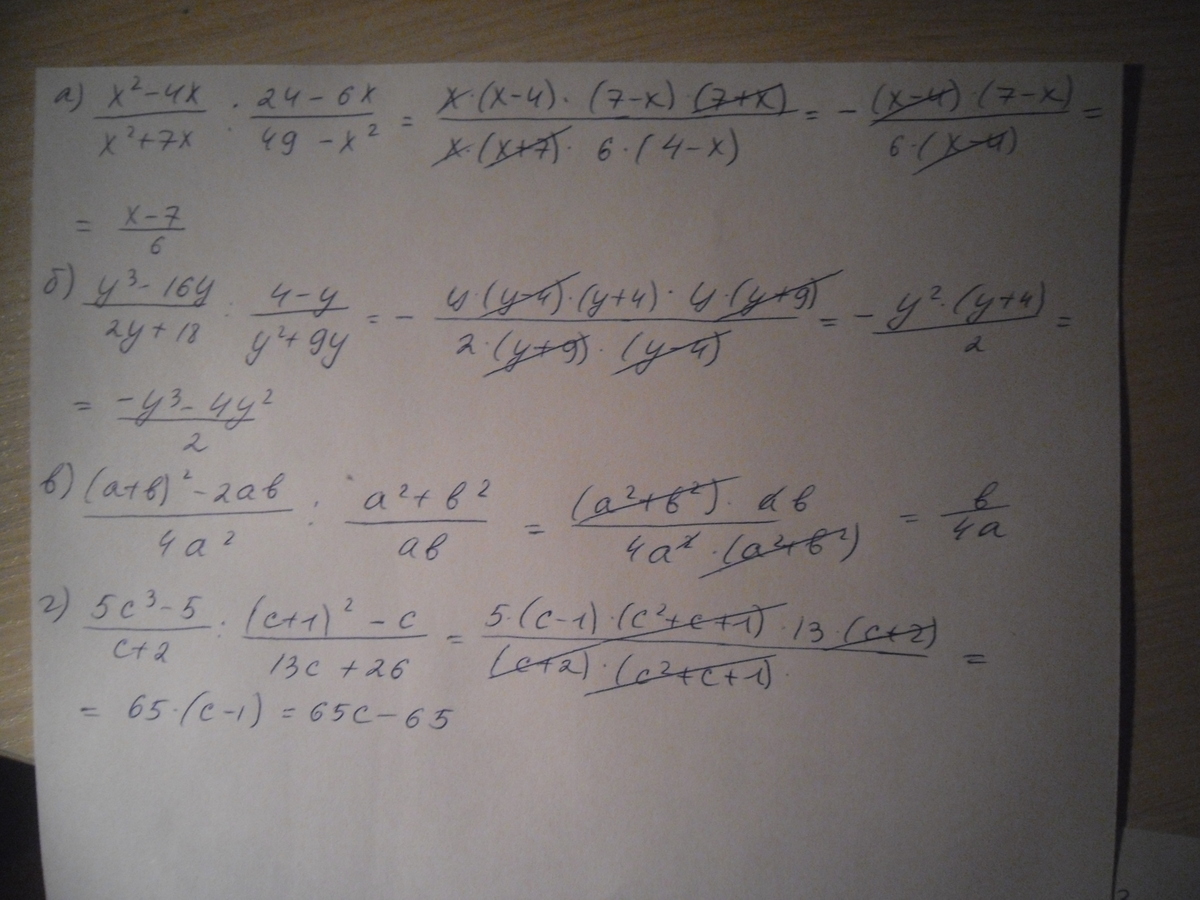
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: emirboy00
Предмет: Окружающий мир,
автор: vedeneevalenv
Предмет: Українська література,
автор: Ruslanruslan11
Предмет: Химия,
автор: lalizhvaniia
Предмет: Математика,
автор: fhxtgji