Предмет: Алгебра,
автор: wereqaska001
(Алгебра 10 класс,мб 9) Докажите что для любых действительных чисел a,b,c,x справедливы неравенства:
Приложения:
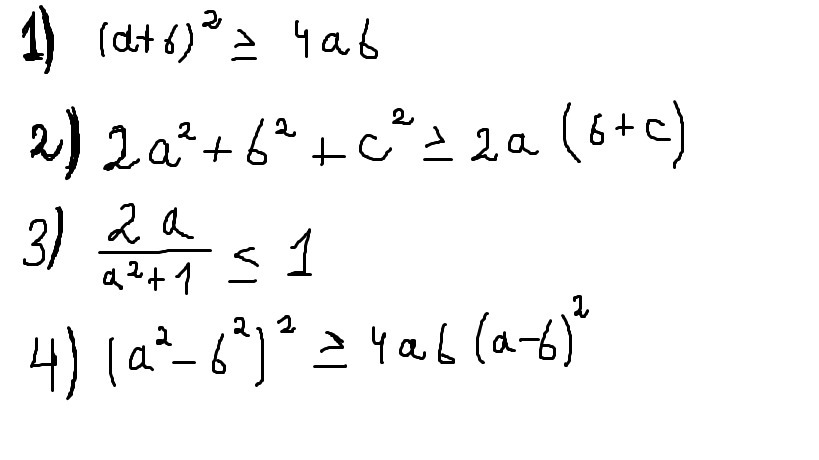
Ответы
Автор ответа:
0
1
(a+b)²-4ab≥0
a²+2ab+b²-4ab≥0
a²-2ab+b²≥0
(a-b)²≥0
Квадрат числа -число всегда положительное или равное 0
2
2a²+b²+c²-2ab-2ac≥0
(a²-2ab+b²)+(a²-2ac+c²)≥0
(a-b)²+(a-c)²≥0
Квадрат числа -число всегда положительное или равное 0⇒сумма положительных-положительна
3
2a/(a²+1)-1≤0
(2a-a²-1)/(a²+1)≤0
(a²-2a+1)/(a²+1)≥0
(a-1)²/(a²+1)>0
Квадрат числа -число всегда положительное или равное 0
Cумма положительных-положительна
Частное положительных-положительно
4
(a-b)²(a+b)²-4ab(a-b)²≥0
(a-b)²[(a+b)²-4ab]≥0
(a-b)²(a²+2ab+b²-4ab)≥0
(a-b)²(a²-2ab+b²)≥0
(a-b)²(a-b)²≥0
(a-b)^4≥0
Число в четной степени всегда больше или равно 0
(a+b)²-4ab≥0
a²+2ab+b²-4ab≥0
a²-2ab+b²≥0
(a-b)²≥0
Квадрат числа -число всегда положительное или равное 0
2
2a²+b²+c²-2ab-2ac≥0
(a²-2ab+b²)+(a²-2ac+c²)≥0
(a-b)²+(a-c)²≥0
Квадрат числа -число всегда положительное или равное 0⇒сумма положительных-положительна
3
2a/(a²+1)-1≤0
(2a-a²-1)/(a²+1)≤0
(a²-2a+1)/(a²+1)≥0
(a-1)²/(a²+1)>0
Квадрат числа -число всегда положительное или равное 0
Cумма положительных-положительна
Частное положительных-положительно
4
(a-b)²(a+b)²-4ab(a-b)²≥0
(a-b)²[(a+b)²-4ab]≥0
(a-b)²(a²+2ab+b²-4ab)≥0
(a-b)²(a²-2ab+b²)≥0
(a-b)²(a-b)²≥0
(a-b)^4≥0
Число в четной степени всегда больше или равно 0
Автор ответа:
0
спасибо огромное
Похожие вопросы
Предмет: Обществознание,
автор: polinarmy57
Предмет: Литература,
автор: atamuhamedovzahongir
Предмет: Химия,
автор: irina112228
Предмет: Биология,
автор: Vuka
Предмет: Алгебра,
автор: Аноним