Предмет: Алгебра,
автор: amberheart
Вычислить. Выбираю лучший ответ.
Приложения:
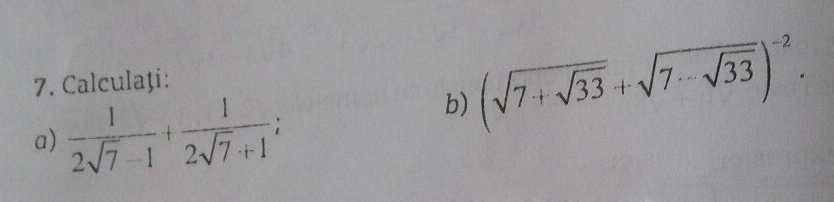
Ответы
Автор ответа:
0
Автор ответа:
0
В моем профиле еще номера, решение которых я тоже отмечу как лучшие, как только будет возможность. (по 15 баллов за каждое задание, в котором 2 примера)
Автор ответа:
0
Отлично, оно мне и нужно
Похожие вопросы
Предмет: Алгебра,
автор: anactacia66
Предмет: История,
автор: qwquuuu
Предмет: Химия,
автор: Аноним
Предмет: Химия,
автор: Kirill270896
Предмет: Математика,
автор: diana2001979