Question

Как решать подобное?
Пусть задана функция f(x) с областью определения [0,1) , найдите область определения функции f( $frac{x}{x+1}$ )

Answer 1

Пусть g(x)=x/(x+1)
Функция f  определена на интервале [0;1).
Найдем, при каких х  дробь x/(x+1) принадлежит указанному интервалу.
Решаем неравенство:
0≤х/(х+1) < 1,
которое равносильно системе неравенств:
{x/(x+1) >0;
{x/(x+1)-1<0.

или
{x/(x+1) >0;
{-1/(x+1)<0.

{x+1>0
{x≥0

Решением данного неравенства является х≥0   или   х∈[0;+∞)

2 способ.
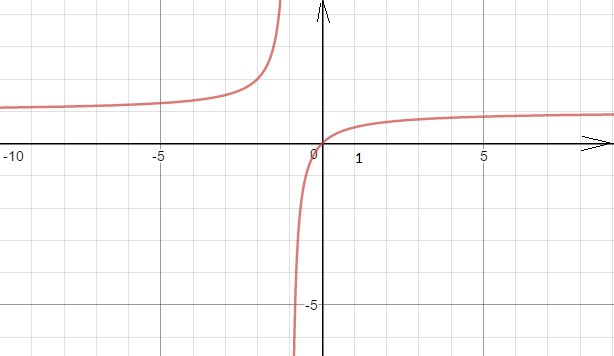
Построим график функции g(x)=x/(x+1).
Выделим целую часть
g(x)=(x+1-1)/(x+1);
g(x)=1-(1/(x+1))- гипербола
Cм. рисунок в приложении
Найдем при каких х  
g(x)∈[0;1)
0≤g(x)<1  ⇒  0≤x< + ∞    
или
х∈[0;+∞)
О т в е т. D(f(x/(x+1))=[0;∞)

Answer 2

т.е. в 10

Answer 3

значит решение начинается с того, что нужно представить х=1 ? и из этого исходить

Answer 4

решение начинается с того, что надо понять, что нам нужны те х, для которых 0<=x/(1+x) <1

Answer 5

а дальше просто решаем это неравенство

Answer 6

Хорошо, благодарю за помощь