Question

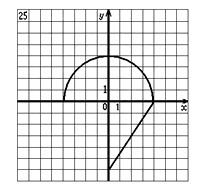
Составить алгоритм, который выдает TRUE, если точка с координатами (х,у) принадлежит к ограниченной области, и FALSE в другом случае.
Помогите с математическим решением, пожалуйста :(((

Answer 1

 Формула уравнения кривой
$frac{x- x_{1} }{ x_{2} - x_{1}} = frac{x- x_{1}}{y_{2} - y_{1}}$

Из нее выводишь уравнение, указанное в условиях в картинке.

Условия внутри скобках будут И
А между собой они будут ИЛИ.

Answer 2

+ в программе не забудь поправку на погрешность действительных чисел ввести.

Answer 3

если не будет получаться - пиши в лс.

Answer 4

Разбиваем область на две.
Первая область располагается, начиная от горизонтальной оси Х и ограничена полуокружностью, т.е. представляет собой полукруг. Радиус окружности равен 4, следовательно её уравнение записывается в виде x²+y²=4², а условие принадлежности точки полукругу выглядит как x²+y²≤16 ∩ x≥0, где ∩ - знак объединения множества точек.
Вторая область - это треугольник, ограниченный полуосью Х, содержащей неотрицательные значения х, полуосью Y, содержащей неположительные значения y и прямой, проходящей через точки с координатами (0;-6) и (4;0). Будем искать уравнение этой прямой в каноническом виде y=kx+b, где k - угловой коэффициент. k=(y₂-y₁)/(x₂-x₁)=(0-(-6))/(4-0)=1.5.
b - это величина вертикального смещения графика относительно оси Х, которая равна значению y при х=0, т.е. -6. Получаем уравнение y=1.5x-6.
Теперь можно записать условие принадлежности точки треугольнику:
y≥1.5x-6 ∩ x≥0 ∩ y≤0.
Осталось объединить эти условия по ИЛИ.
(x²+y²≤16 ∩ x≥0) ∪ (y≥1.5x-6 ∩ x≥0 ∩ y≤0)
Здесь есть общее условие x≥0, поэтому выражение можно упростить.
x≥0 ∩ (x²+y²≤16 ∪ y≥1.5x-6 ∩ y≤0)
Словесно алгоритм можно записать так.
x≥0 И [x²+y²≤16 ИЛИ (y≥1.5x-6 И y≤0)]
Поскольку это логическое выражение, его значением будет TRUE или FALSE, поэтому никаких дополнительных присваиваний не требуется.