Предмет: Математика,
автор: hwuw
Сколько корней имеет заданное уравнение при указанных ограничениях на параметр а:
а)x^3-3x^2=a , -4<a<0
б)-x^3+3x^2-2=a , a<-2
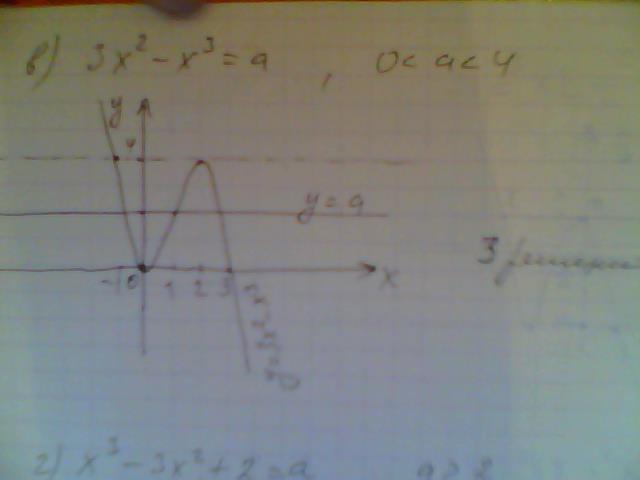
в)3x^2-x^3=a, 0<a<4
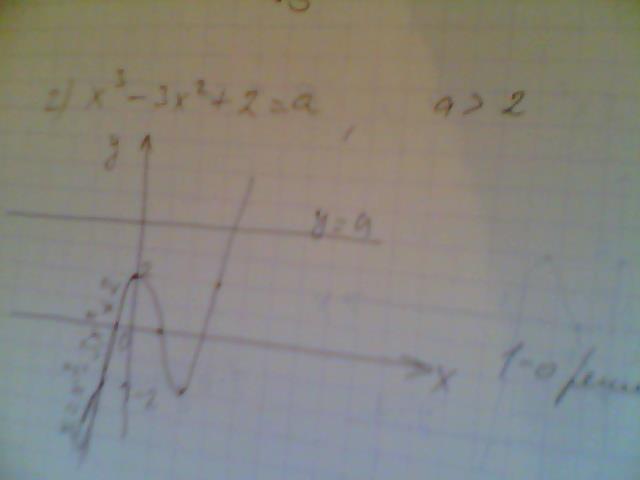
г)x^3-3x^2+2=a , a>2
Ответы
Автор ответа:
0
Все эти задания можно выполнить следующим образом: построить графики левой и правой частей: График правой части - это прямая параллельная оси Х, пробегает значения от -4 до 0. По графику видно, что она пересекает график функции, заданной левой частью уравнения в трех точках, значит уравнение а) имеет 3 решения при указанных ограничениях а. б) одно решение; в) 3 решения; г) одно решение. Графики во вложениях. Надеюсь, что решение будет лучшим.
Приложения:

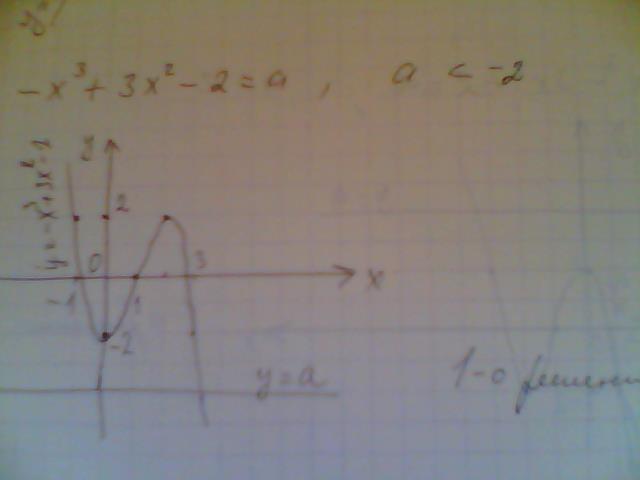
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Другие предметы,
автор: Аноним
Предмет: Геометрия,
автор: ngolden596
Предмет: Математика,
автор: МироСлавочкa