Question

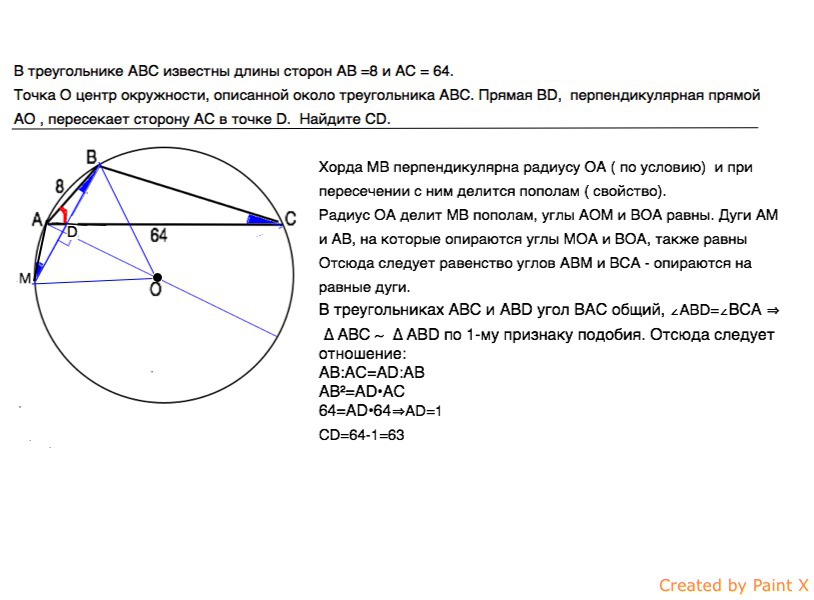
В треугольнике АВС известны длины сторон АВ =8 и АС = 64.
Точка О центр окружности, описанной около треугольника АВС. Прямая ВD перпендикулярная прямой АО , пересекает сторону АС в точке D. Найдите СD.

Answer 1

В треугольнике АВС известны длины сторон АВ =8 и АС = 64.

Точка О центр окружности, описанной около треугольника АВС. Прямая ВD  перпендикулярная прямой АО , пересекает сторону АС в точке D. Найдите СD.

–––––––––––––––––

Продлим ВD до пересечения с окружностью в точке М. 

Хорда МВ перпендикулярна радиусу ОА ( по условию)  и при пересечении с ним делится пополам ( свойство). 

Тогда  радиус ОА делит угол ВОМ пополам. Дуги АМ и АВ, на которые опираются равные центральные углы МОА и ВОА, также равны. 

Отсюда следует равенство углов АВМ и ВСА - опираются на равные дуги. 

В треугольниках АВС и АВD угол ВАС общий, ∠АВD=∠ВСА ⇒

 ∆ АВС ~  ∆ АВD по 1-му признаку подобия. Из подобия следует отношение:

АВ:АС=АD:АВ

АВ²=АD•AC

64=AD•64⇒  AD=1

CD=64-1=63 (ед. длины)