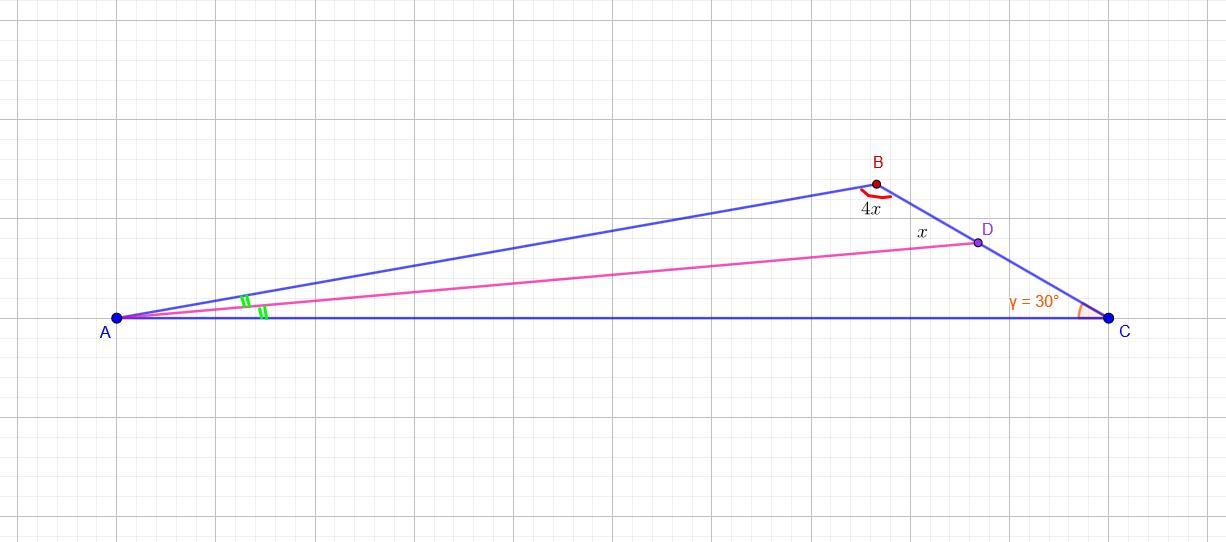
В треугольнике ABC угол C равен 30, AD-биссектриса угла A, угол B больше угла ADB в четыре раза. Найдите градусную меру угла B.
Ответы
Дано:
ΔABC, ∠C = 30°, AD - биссектриса ∠A, ∠ABC = 4 ∠ADB.
Чертеж в приложении.
Найти:
∠B - ?
Решение:
Пусть ∠ADB = x. Тогда ∠ABC = 4x. По теореме о сумме углов треугольника (смотрите на ΔABD):
∠BAD = 180° - ∠ADB - ∠ABC = 180° - x - 4x = 180° - 5x.
А про углы ΔADC можно сказать следующее:
∠ACD = 30° (написано в условии);
∠ADC = 180° - ∠ADB = 180° - x (∠ADC и ∠ADB - смежные);
∠CAD = 180° - ∠ACD - ∠ADC = 180° - 30° - (180° - x) = x - 30° (уже упомянутая в решении теорема о сумме углов треугольника, и несложные алгебраические преобразования).
А теперь вспомним, что AD биссектриса:
∠BAD = ∠CAD
180° - 5x = x - 30°
x + 5x = 180° + 30°
6x = 210°
x = 35°
Теперь несложно найти ∠B:
∠B = ∠ABC = 4x = 4 · 35° = 140°.
Задача решена!
Ответ: ∠B = 140°.