Предмет: Алгебра,
автор: AlinaMalinaa11
Найдите угловой коэффициент касательной к графику функции y=f(x) в точке с абсциссой x0:
Приложения:
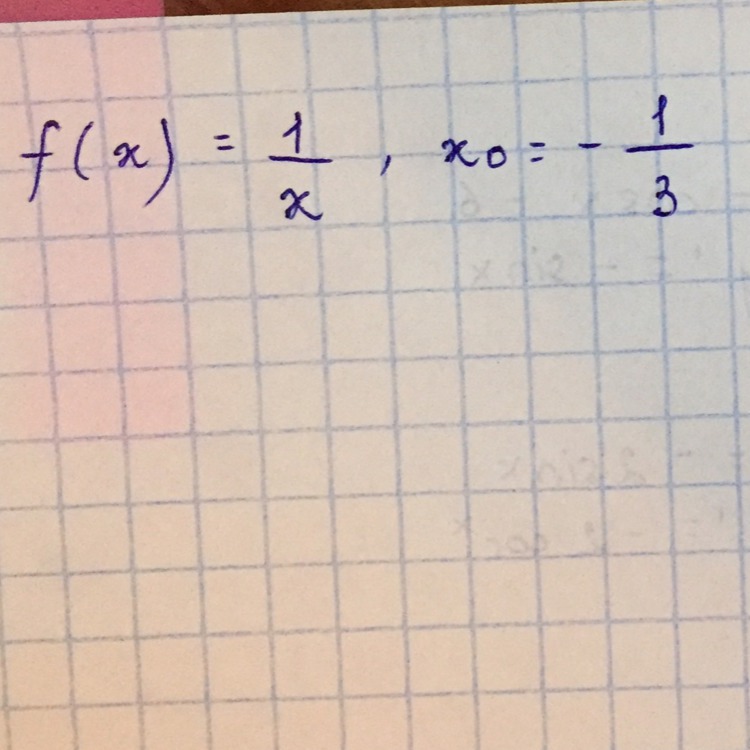
Ответы
Автор ответа:
0
Угловой коэффициент- это значение производной в точке касания. Значит, что делаем? Ищем производную и в неё подставим х₀
Поехали...
f(x) = 1/x = x ⁻¹
f'(x) = -1*x⁻² = -1/x²
f'(x₀) = f'(-1/3) = -1 : 1/9 = -9
Поехали...
f(x) = 1/x = x ⁻¹
f'(x) = -1*x⁻² = -1/x²
f'(x₀) = f'(-1/3) = -1 : 1/9 = -9
Автор ответа:
0
Для вычисления углового коэффициента касательной к графику функции в некоторой точке этого графика нужно вычислить значение производной функции в этой точке. Следовательно,  искомый угловой коэффициент касательной равен
искомый угловой коэффициент касательной равен 
Похожие вопросы
Предмет: Английский язык,
автор: aleksq0510
Предмет: Химия,
автор: alinakondratuk12345
Предмет: Другие предметы,
автор: majtanovaamina3
Предмет: Математика,
автор: timser751
Предмет: Математика,
автор: VIKТ0R