Предмет: Алгебра,
автор: натаня07
помогите пожайлуста
Приложения:
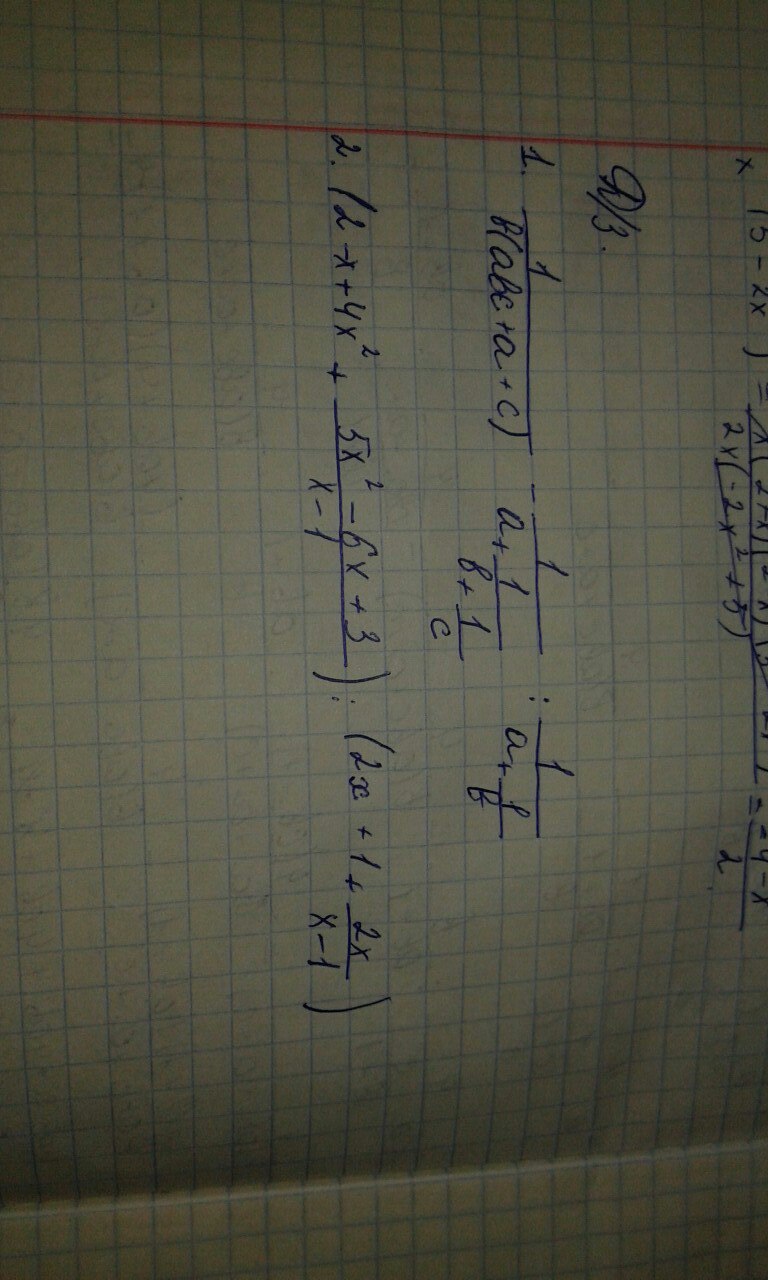
Ответы
Автор ответа:
0
почерк красивый))) хех
Автор ответа:
0
спасибо
Автор ответа:
0
а какой это класс?
Автор ответа:
0
это колледж 9 10
Автор ответа:
0
а ясно)
Автор ответа:
0
Автор ответа:
0
извините что только первое, не надо было мне начинать решать.
Автор ответа:
0
все ровно спасибо это правильно??
Похожие вопросы
Предмет: География,
автор: unknown777797
Предмет: Математика,
автор: amalyamakhanashvili
Предмет: Математика,
автор: Vik0923
Предмет: Математика,
автор: forestersys
Предмет: Физика,
автор: LolandLol