Предмет: Алгебра,
автор: Superiorintelligent
(2 +√(5))^(1/3) + (2 -√(5))^(1/3)
Приложения:
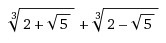
Ответы
Автор ответа:
0
Методом подбора получаем корень последнего уравнения А=1. Делим левую часть уравнения на (А-1), получим А²+А+4, тогда
Похожие вопросы
Предмет: История,
автор: alexandra10102
Предмет: Математика,
автор: vbilan480
Предмет: Биология,
автор: karamelika0908
Предмет: Литература,
автор: lenovilo5566