Предмет: Алгебра,
автор: ГОСТЬ2014
Помогите решить под 2 и 3
Приложения:
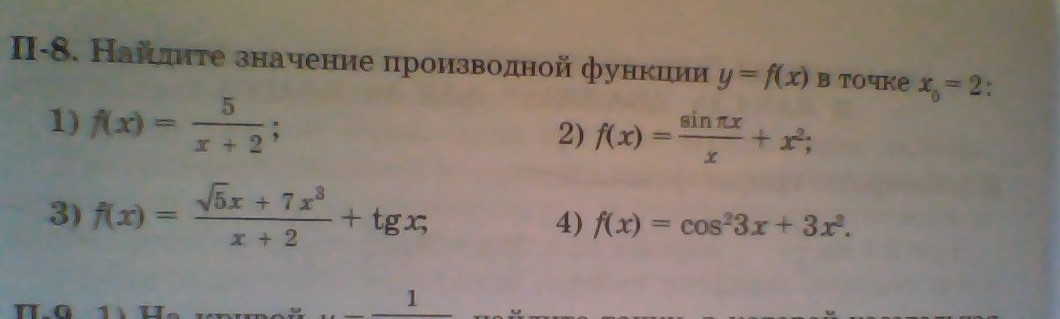
Ответы
Автор ответа:
0
2
![f'(x)=( frac{sin( pi x)}{x} +x^2)'=[x^{-1}*sin( pi x)]'+2x= f'(x)=( frac{sin( pi x)}{x} +x^2)'=[x^{-1}*sin( pi x)]'+2x=](https://tex.z-dn.net/?f=f%27%28x%29%3D%28+frac%7Bsin%28+pi+x%29%7D%7Bx%7D+%2Bx%5E2%29%27%3D%5Bx%5E%7B-1%7D%2Asin%28+pi+x%29%5D%27%2B2x%3D)




3
![f'(x)=[(x+2)^{-1}*( sqrt{5}x+7x^3 )+tg(x)]'= f'(x)=[(x+2)^{-1}*( sqrt{5}x+7x^3 )+tg(x)]'=](https://tex.z-dn.net/?f=f%27%28x%29%3D%5B%28x%2B2%29%5E%7B-1%7D%2A%28+sqrt%7B5%7Dx%2B7x%5E3+%29%2Btg%28x%29%5D%27%3D)
![=[(x+2)^{-1}]'*( sqrt{5}x+7x^3 )+(x+2)^{-1}*[( sqrt{5}x+7x^3 )]'+(tg(x))'= =[(x+2)^{-1}]'*( sqrt{5}x+7x^3 )+(x+2)^{-1}*[( sqrt{5}x+7x^3 )]'+(tg(x))'=](https://tex.z-dn.net/?f=%3D%5B%28x%2B2%29%5E%7B-1%7D%5D%27%2A%28+sqrt%7B5%7Dx%2B7x%5E3+%29%2B%28x%2B2%29%5E%7B-1%7D%2A%5B%28+sqrt%7B5%7Dx%2B7x%5E3+%29%5D%27%2B%28tg%28x%29%29%27%3D)




3
Автор ответа:
0
можно было еще в 3-м немножко сократить подобные слагаемые но мы на это уже закроем глаза. спасибо за труд.
Автор ответа:
0
вы лучше подскажите, с чем связано появление < span>
Автор ответа:
0
пока что не понимаю
Автор ответа:
0
вылез глюк, оставляем все как есть - пример решен
Автор ответа:
0
так что вы знаете про этот глюк?
Похожие вопросы
Предмет: Другие предметы,
автор: aigul8418t
Предмет: Русский язык,
автор: gogagoga75
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: koshelevanadia
Предмет: Физика,
автор: assashi2015