Предмет: Геометрия,
автор: dsl13011970Sveta
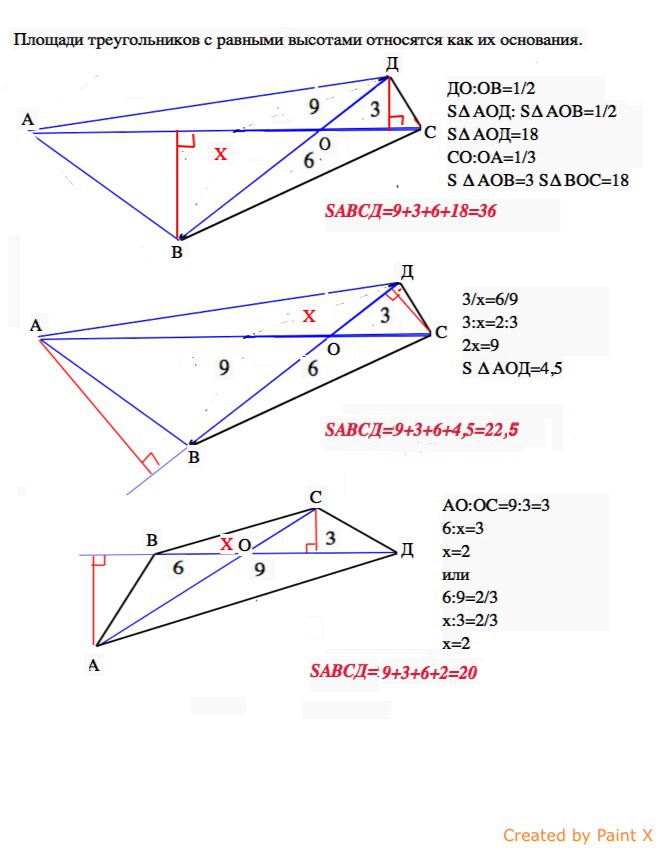
Диагонали выпуклого четырехугольника делят его на 4 треугольника. Площади трех из них равны 3, 6, 9. Найдите площадь четырехугольника
Ответы
Автор ответа:
0
решение смотри в файле
Приложения:

Автор ответа:
0
Вариант решения.
Из свойств площадей треугольников:
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований.
Для данного по условию четырехугольника справедливыми будут три ответа - в зависимости от того, в каком порядке расположены части, получившиеся при пересечении диагоналей.
Подробнее в приложении.
Из свойств площадей треугольников:
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований.
Для данного по условию четырехугольника справедливыми будут три ответа - в зависимости от того, в каком порядке расположены части, получившиеся при пересечении диагоналей.
Подробнее в приложении.
Приложения:
Автор ответа:
0
ок, только там во втором - описка в ответе
Автор ответа:
0
Спасибо, исправила.
Автор ответа:
0
это если диагонали пересекутся под прямым углом,а если нет
Автор ответа:
0
Диагонали пересекаются "как хотят". Угол не важен...
Автор ответа:
0
Угол между диагоналями в этой задаче неважен. Отношение площадей треугольников с равными высотами позволяет найти площадь четвертого треугольника, а искомая площадь - сумма всех треугольников, из которых он состоит. В решении диагонали не пересекаются под прямым углом.
Похожие вопросы
Предмет: Математика,
автор: VenomOff
Предмет: Английский язык,
автор: sonya2712928
Предмет: Геометрия,
автор: Kaftofka
Предмет: Обществознание,
автор: salimyanovanat
Предмет: Физика,
автор: Furande