Question

Бак атомобиля полностью заполнен бензином. К дну привязана нитью пробка, «парящая» в бензине. На какой угол отклонится пробка на нити при длительном движении автомобиля вправо с постоянным ускорением а. Желателен чертеж.

Answer 1

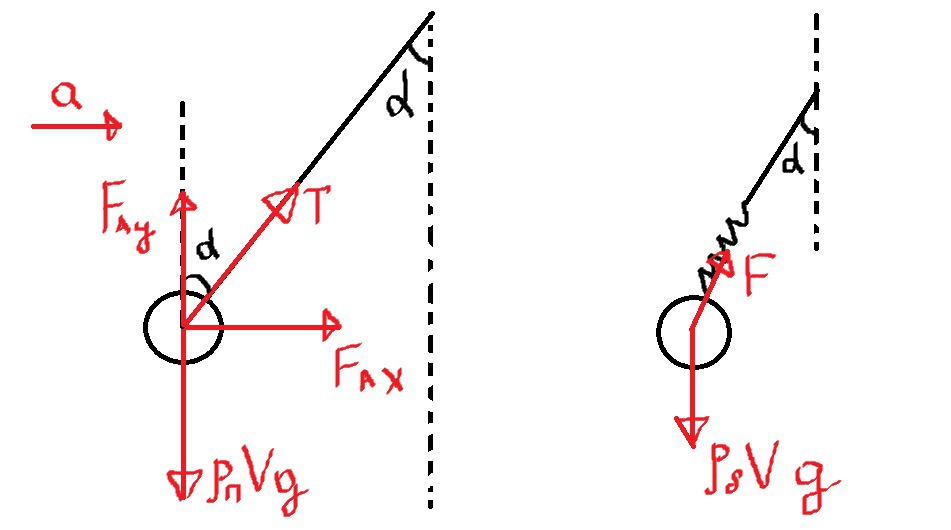
• чертеж в приложении. задача довольно стандартная, если не учитывать, что направление Архимедовой силы - не вертикальное, и в данном случае ее значение нужно искать как вес вытесненного бензина

• проведем мысленный эксперимент: подвесим "шар" бензина к пружинке динамометра. тогда сила упругости F, возникающая в этой пружинке, будет численно равна по 3 закону Ньютона весу нашего шара, и, соответственно, Архимедовой силе

• написав уравнение динамики для нашего шара в проекции на вертикальную ось, получим:

○ F = (p(б) V g)/cosα = Fa, где p(б) - плотность бензина, V - объем шара (я сейчас припомнил, что у нас в задаче фигурирует пробка, но ничего)

• соответственно, проекции Архимедовой силы на горизонтальную и вертикальную оси равны:

○ Fa(x) = p(б) V g
○ Fa(y) = p(б) V g tgα

• напишем уравнения для горизонтальной и вертикальной осей для нашей пробки:

○ Tcosα + p(б) V g = p(п) V g, где p(п) - плотность пробки
○ Tsinα + p(б) V g tgα = p(п) V a

• выражая силу натяжения нити и приравнивая выражения, получаем:

○ cosα (p(п) V a - p(б) V g tgα) = sinα (p(п) V g - p(б) V g)

• дeлим обе части на cosα. после этого нетрудно получить ответ:

○ tgα = a/g

Answer 2

Верно подмечено, Но для его решения рис пойдет.

Answer 3

А вот проще как? я не понял.

Answer 4

я тоже. почему при не полностью заполненном баке задача упрощается? там еще и, по идее, объем погруженной части пробки нужно искать :/

Answer 5

написано выше: "...К нам иногда некоторые "ваши" придираются..." . отвечу за "наших": если Вы придирками считаете устные замечания и пожелания, то прийдется молча ставить предупреждения и баны например за флуд в комментариях

Answer 6

для разрядки обстановки предлагаю решить устно http://znanija.com/task/5630088 и кинуть мне в личку ответ