Предмет: Алгебра,
автор: LiraReimand
Очень оченьочень очень очень очень нужно ))
Приложения:
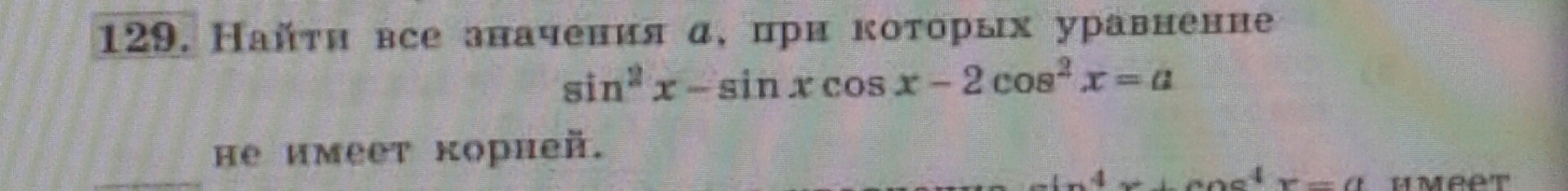
Ответы
Автор ответа:
0
Sin²x - SinxCosx - 2Cos²x = a*1
Sin²x - SinxCosx - 2Cos²x = a( Sin²x + Cos²x)
Sin²x - SinxCosx - 2Cos²x = aSin²x + aCos²x
Sin²x - SinxCosx - 2Cos²x - aSin²x - aCos²x = 0
Sin²x(1 - a) -SinxCosx -Cos²x(2 + a) = 0 |: Cos²x≠0
tg²x (1-a) - tgx - (2+a) = 0
tgx = z
z²(1-a) -z -(2 +a) = 0
D = b² - 4ac = 1 + 4*(1 -a)(2 +a)= 1 + 8 - 8a +4a -4a² = -4a² -4a +9
Уравнение не имеет решения при D < 0
-4a² - 4a +9 < 0
а₁ = (2 +-√(4+36))/-4 = (2 +-2√10)/-4= (-1+-√10)/2
а∈(-∞; (-1-√10)/2)∪( (-1+√10)/2; +∞)
Sin²x - SinxCosx - 2Cos²x = a( Sin²x + Cos²x)
Sin²x - SinxCosx - 2Cos²x = aSin²x + aCos²x
Sin²x - SinxCosx - 2Cos²x - aSin²x - aCos²x = 0
Sin²x(1 - a) -SinxCosx -Cos²x(2 + a) = 0 |: Cos²x≠0
tg²x (1-a) - tgx - (2+a) = 0
tgx = z
z²(1-a) -z -(2 +a) = 0
D = b² - 4ac = 1 + 4*(1 -a)(2 +a)= 1 + 8 - 8a +4a -4a² = -4a² -4a +9
Уравнение не имеет решения при D < 0
-4a² - 4a +9 < 0
а₁ = (2 +-√(4+36))/-4 = (2 +-2√10)/-4= (-1+-√10)/2
а∈(-∞; (-1-√10)/2)∪( (-1+√10)/2; +∞)
Похожие вопросы
Предмет: Алгебра,
автор: maksserak605
Предмет: Математика,
автор: asansabina0865
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: 867903
Предмет: Литература,
автор: mrchildren05