Предмет: Алгебра,
автор: AlisNK
помогите с решение 31 уравнения.
Приложения:
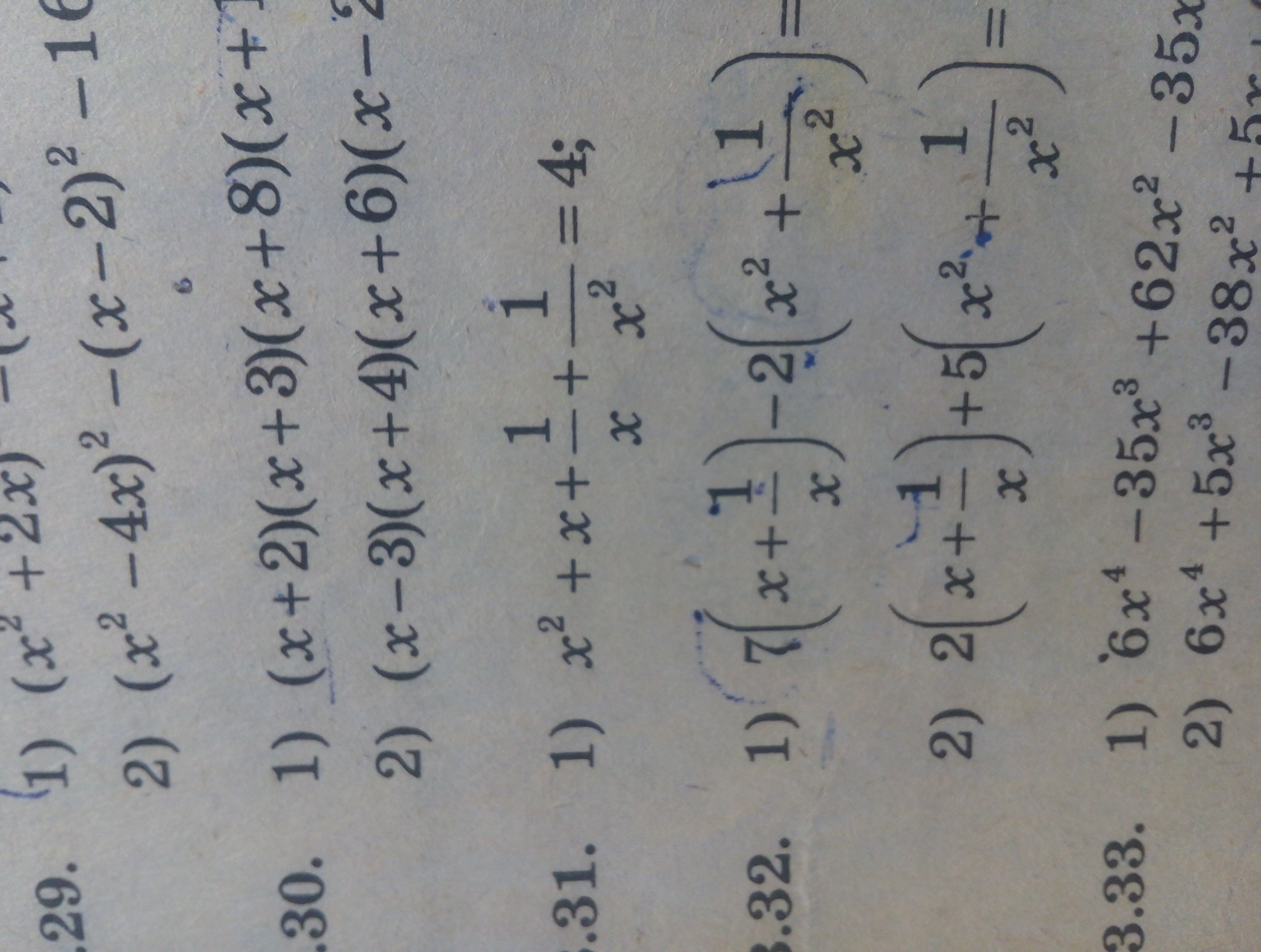
Ответы
Автор ответа:
0
Замена переменной
х+(1/х)=t;
x²+2+(1/x²)=t² ⇒ x²+(1/x²)=t² - 2
Уравнение принимает вид:
t²- 2 + t=4
t²+t - 6=0
D=1-4·(-6)=1+24=25
t=(-1+5)/2=2 или t=(-1-5)/2=-3
x+(1/x)= 2 ⇒ x²-2x+1=0 (x-1)²=0 x= 1
x+(1/x)=- 3 ⇒ x² + 3x+1=0 D=5 x=(-3-√5)/2 или х=(-3+√5)/2
О т в е т. х=1; х=(-3-√5)/2; х=(-3+√5)/2.
х+(1/х)=t;
x²+2+(1/x²)=t² ⇒ x²+(1/x²)=t² - 2
Уравнение принимает вид:
t²- 2 + t=4
t²+t - 6=0
D=1-4·(-6)=1+24=25
t=(-1+5)/2=2 или t=(-1-5)/2=-3
x+(1/x)= 2 ⇒ x²-2x+1=0 (x-1)²=0 x= 1
x+(1/x)=- 3 ⇒ x² + 3x+1=0 D=5 x=(-3-√5)/2 или х=(-3+√5)/2
О т в е т. х=1; х=(-3-√5)/2; х=(-3+√5)/2.
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: safroniychuk
Предмет: Литература,
автор: beded68
Предмет: Геометрия,
автор: xxguthrie
Предмет: Биология,
автор: anastasiasykah12