Предмет: Алгебра,
автор: kokos1895
Пожалуйста решите )))
Приложения:
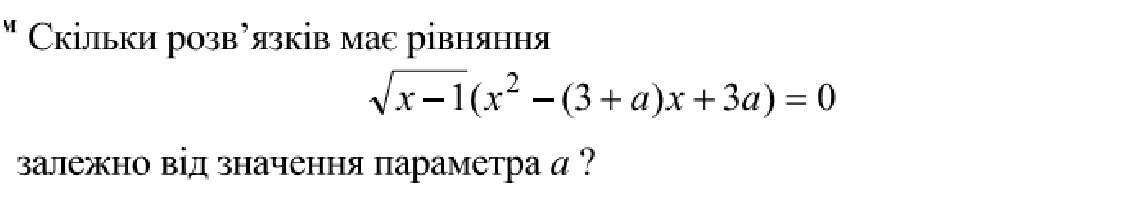
Ответы
Автор ответа:
0
ОДЗ:
Произведение равно нулю
Если D=0, то квадратное уравнение имеет 2 действительных корней, но нужно учтить ОДЗ. Найдем корни квадратного уравнения
Решим неравенства отдельно
очевидно, что при любых а выполняется неравенство
Если D=0, то квадратное уравнение имеет одно решение
a-3=0
a=3 -
При
При
Автор ответа:
0
Спасибо
Похожие вопросы