Предмет: Алгебра,
автор: Romanova3
помогите с решением, пожалуйста
Приложения:
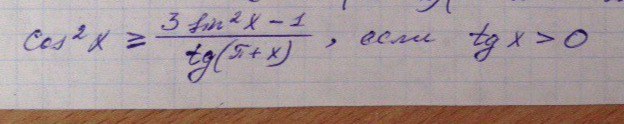
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: lalklullabkbkbkb
Предмет: Литература,
автор: vikisky2007
Предмет: Физика,
автор: masha202059
Предмет: Информатика,
автор: lolita996
Предмет: Математика,
автор: muratovaarina2