Question

срочно. 6 балов дам .......

Answer 1

Задание 1.

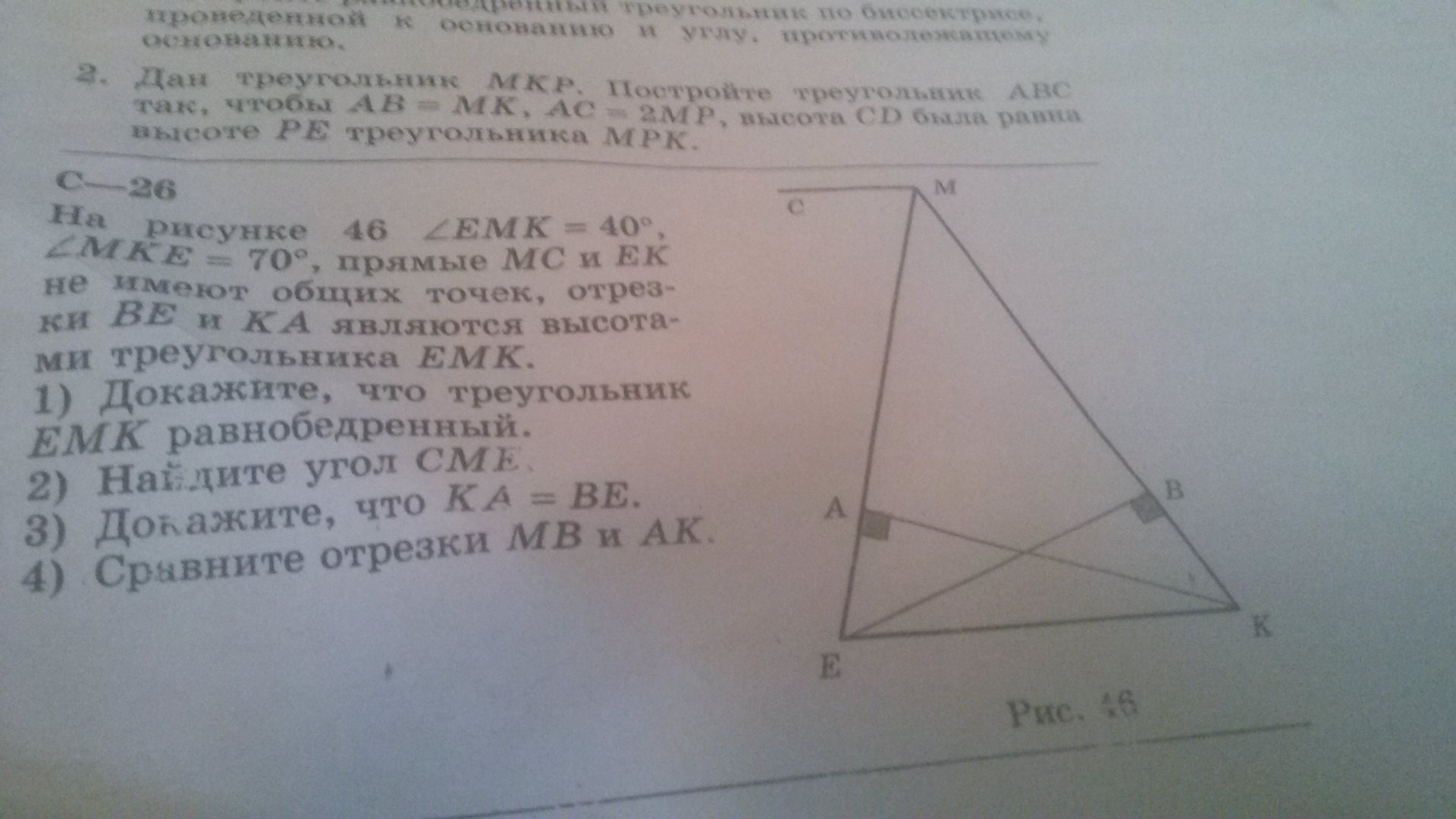
CM║EK. ∠CME = ∠MEK = (180°-40°) :2 = 70° как накрест лежащие ⇒ ∠MEK =∠MKE, углы при основании раны⇒ ΔEMK равнобедренный. ч.т.д.

Задание 2.

∠СМЕ = (180°-40°):2 = 140° :2= 70

Задание 3.

∠К=∠Е. ∠ВЕК = 90°-∠К = 90°-∠Е =∠АКЕ. ЕК - общая сторона ⇒ΔАКЕ =ΔВКЕ по стороне и двум углам ⇒КА=ВЕ ч.т..д.

Задание 4.

МВ=МА. Рассмотрим треугольник МАК. ∠АМК=40° по условию, ∠МАК=90° по условию. ∠МКА=90°-40°=50°. Против большей стороны лежит больший угол. МА=МВ>АК. 
Ответ: Мв больше АК

Answer 2

1. Из равенства треугольников АЕК и ВКЕ
Доказательство:
-Угол ЕАК и ЕВК равны. Исходя из условий задачи
-Треугольники АЕО и ВКО равнобедренны и равны, так как углы ЕАО и КВО равны, исходя из условий задачи, и равны углы АОЕ и ВОК, так как они вертикальные. Равнобедренны, потому что углы при основании равны, исходя из сравнения ЕА/КВ=АО/ВО=ЕО/КО, но это не важно. Следовательно, равны стороны ЕА и ВК.
Значит, треугольники равны.
Следовательно, угол МКЕ = МЕК = 70°. Тр. ЕМК равнобедренный
2. СМЕ = (180-40) : 2 = 70°
3. Из доказательства равенства тр. АЕК и ВКЕ
4. В этом я не шарю