Question

СРОЧНО НУЖНО
ПОМОГИТЕ
докажите, что в равнобедренном треугольнике медианы, проведенные к равны сторонам равны.

Answer 1

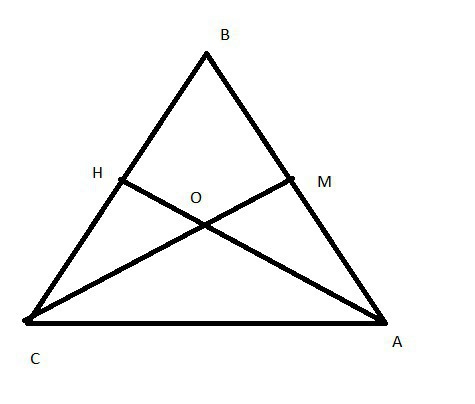
Дан треугольник АВС(СВ=ВА) СМ,АН - медианы.
Медиана в треугольнике делит сторону, к которой она проведена, на два равных отрезка.
АМ=МВ=СН=НВ (так как СВ=ВА)
Рассмотрим треугольники НАС и МАС 
В них:
∠А=∠С (углы при основании р/б)
МА=НС 
СА - общая сторона 
Значит, рассматриваемые треугольники равны по первому признаку(по двум сторонам и углу между ними)
В равных треугольниках соответственные стороны равны т.е НА=СМ, что и требовалось доказать.