Предмет: Математика,
автор: ттттттттт3
люди,кто не спит!очень нужно решение
Приложения:
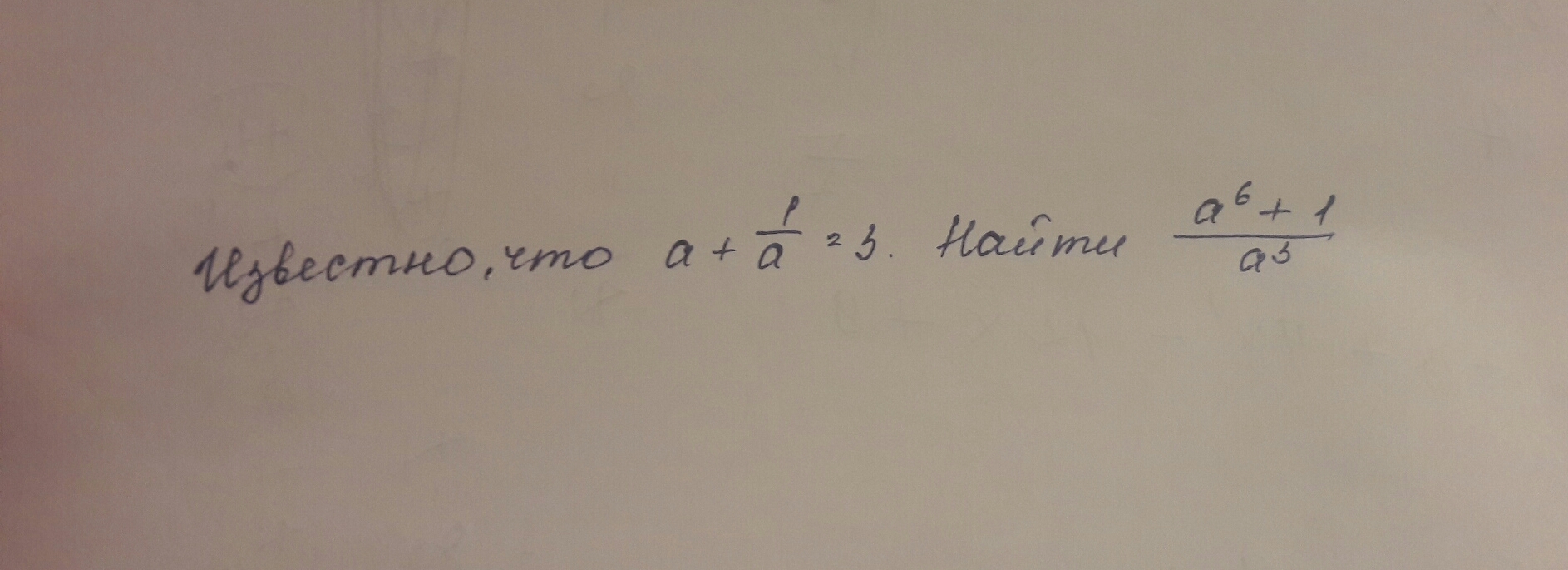
Ответы
Автор ответа:
0
Дано: 
Найти:
решение:


возведем в куб

преобразуем левую часть

второе слагаемое равно из дано, подставим:
из дано, подставим:



Найти:
решение:
возведем в куб
преобразуем левую часть
второе слагаемое равно
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: bvbvdvlvlvlv
Предмет: Алгебра,
автор: kotaras
Предмет: Химия,
автор: vanilka2115
Предмет: Биология,
автор: krotenok1990
Предмет: Математика,
автор: Zalyalulu