Предмет: Математика,
автор: chikunoveugene
помогите пожалуйста решить 14е задание. геометрия
Приложения:
Ответы
Автор ответа:
0
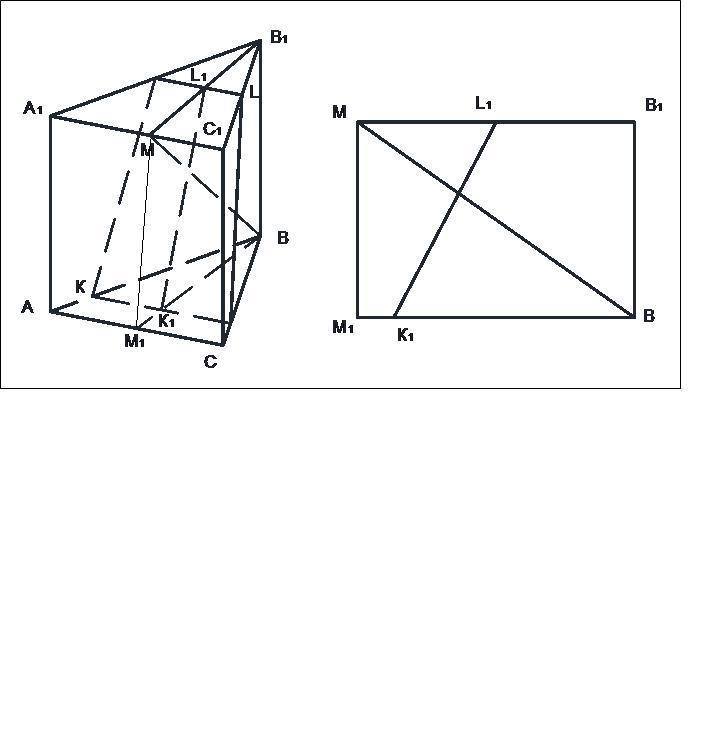
а) Проведём сечение призмы через ребро ВВ1 перпендикулярно АС.
Так как заданная плоскость γ параллельна АС, то наше сечение перпендикулярно плоскости γ и в нём лежит заданное расстояние от точки В до плоскости γ.
Плоскость γ в нашем сечении будет линией сечения L1K1.
Сечение - это прямоугольник М1МВ1В.
Высота его равна высоте призмы и равна 3.
Длина - это высота основания и равна для равностороннего треугольника а√3/2 = 6*√3/2 = 3√3.
Точка L1 лежит на середине МВ1.
М1К1 равно 1/6 М1В.
Определяем тангенсы углов наклона отрезков МВ и L1К1 к основанию.
tg(<МВМ1) = 3/(3√3) = 1/√3.
tg(<L1К1В) = 3/(3√3-(3√3/6)-3√3/2)) = 3/(6√3/6) = 3/√3 = √3.
Так как тангенсы углов наклона отрезков взаимно обратны, то то это признак перпендикулярности этих отрезков.
Это доказывает, что прямая ВМ перпендикулярна плоскости γ.
По тангенсам углов определяем их величины:
<МВМ1 = 30°, <L1К1В = 60°.
б) BM = √(3²+(3√3)²) = √(9+27) = √36 = 6.
MM2 = ML1*cos30° = (3√3/2)*(√3/2) = 3.
Искомое расстояние от точки В до плоскости γ равно 6-3 = 3.
Так как заданная плоскость γ параллельна АС, то наше сечение перпендикулярно плоскости γ и в нём лежит заданное расстояние от точки В до плоскости γ.
Плоскость γ в нашем сечении будет линией сечения L1K1.
Сечение - это прямоугольник М1МВ1В.
Высота его равна высоте призмы и равна 3.
Длина - это высота основания и равна для равностороннего треугольника а√3/2 = 6*√3/2 = 3√3.
Точка L1 лежит на середине МВ1.
М1К1 равно 1/6 М1В.
Определяем тангенсы углов наклона отрезков МВ и L1К1 к основанию.
tg(<МВМ1) = 3/(3√3) = 1/√3.
tg(<L1К1В) = 3/(3√3-(3√3/6)-3√3/2)) = 3/(6√3/6) = 3/√3 = √3.
Так как тангенсы углов наклона отрезков взаимно обратны, то то это признак перпендикулярности этих отрезков.
Это доказывает, что прямая ВМ перпендикулярна плоскости γ.
По тангенсам углов определяем их величины:
<МВМ1 = 30°, <L1К1В = 60°.
б) BM = √(3²+(3√3)²) = √(9+27) = √36 = 6.
MM2 = ML1*cos30° = (3√3/2)*(√3/2) = 3.
Искомое расстояние от точки В до плоскости γ равно 6-3 = 3.
Приложения:
Автор ответа:
0
Расстояние надо найти от точки С, а не от точки В. На чертеже не обозначена точка М2.
Автор ответа:
0
Расстояние Н от точки С до плоскости гамма равно расстоянию от точки М1. H = М1К1*cos30 = (1/6)*(3√3)*(√3/2) = 3/4.
Похожие вопросы
Предмет: Физика,
автор: olya1232579
Предмет: Математика,
автор: muhametkanovmansur
Предмет: Алгебра,
автор: fokatom0
Предмет: Обществознание,
автор: verastarovoytova
Предмет: Математика,
автор: eneta