Question

Через точку Р,лежащую внутри окружности,проведена хорда,которая делится точкой Р на отрезки,длины которых равны 4 и 5 см.Найти расстояние от точки P до центра окружности,если ее радиус равен 6 см.

Answer 1

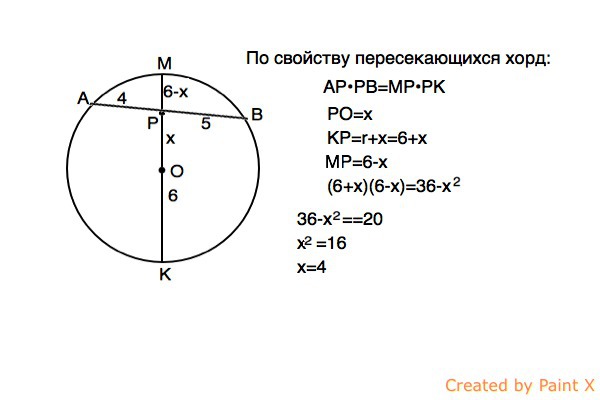
Если хорды пересекаются, то произведения их отрезков, на которые их разделила точка пересечения, равны. 
Диаметр - наибольшая хорда. 
Пусть хорда - АВ, диаметр, проходящий через т.Р - МК. 
АР=4, ВР=5. 
Примем искомое расстояние РО=х
Тогда КР=r+х=6+х
МР=r-х=6-х⇒
4•5=(6+х)•(6-х)⇒
х²=36-20 ⇒
х=√16=4
ОР=4