Предмет: Геометрия,
автор: Sergo228322
в треугольнике ABC провели биссектрису CK, а в треугольнике BCK - биссектрису KL. прямые AC и KL пересекаются в точке M. извесно, что ∠BAC > ∠BCA. докажите, что AK + KC > AM.
Ответы
Автор ответа:
0
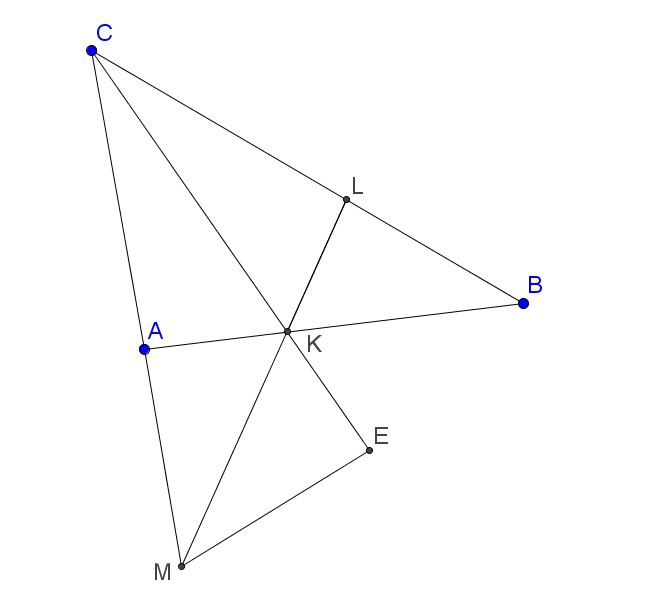
1) На продолжении СК за точку К возьмем точку Е так, что KE=AK, т.е. AK+KC=CE.
2) Т.к. KL - биссектриса ∠CKB и углы AKC и EKB вертикальные, то ∠AKM=∠EKM и соответственно треугольники AKM и EKM равны по 1-му признаку. Значит, AM=ME.
3) ∠CME=180°-∠MCE-∠MEC=180°-∠C/2-(180°-∠A)=∠A-∠C/2. Т.к. по условию ∠A-∠C/2>∠C/2, то ∠CME>∠MCE и значит СE>ME (т.к. в треугольнике напротив большего угла лежит большая сторона), т.е. в силу 1) и 2) получаем AK+KC>AM.
2) Т.к. KL - биссектриса ∠CKB и углы AKC и EKB вертикальные, то ∠AKM=∠EKM и соответственно треугольники AKM и EKM равны по 1-му признаку. Значит, AM=ME.
3) ∠CME=180°-∠MCE-∠MEC=180°-∠C/2-(180°-∠A)=∠A-∠C/2. Т.к. по условию ∠A-∠C/2>∠C/2, то ∠CME>∠MCE и значит СE>ME (т.к. в треугольнике напротив большего угла лежит большая сторона), т.е. в силу 1) и 2) получаем AK+KC>AM.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: margosha6999
Предмет: Математика,
автор: oigafin86
Предмет: Русский язык,
автор: danillee129
Предмет: Химия,
автор: dota2forever
Предмет: Биология,
автор: zatworld3