Предмет: Математика,
автор: gontar1987
ПОМОГИТЕ С ТЕОРИЕЙ ВЕРОЯТНОСТИ . ПЛИЗЗ . только по факту кто разбирается.В одном районе республики 24 человека обучаются на заочном отделении института, из них 6 на юридическом факультете, 12 на экономическом и 6 на факультете «Налоговое дело». Вероятность успешно сдать все экзамены на предстоящей сессии для студентов юрфака равна 0,6, экономфака - 0,76, для студентов факультета «Налоговое дело» - 0,8. Найти вероятность того, что наудачу взятый студент, успешно сдавший все экзамены, будущий «налоговик».
Ответы
Автор ответа:
0
найдем вероятность С (1;6)×0,8/(С (1;6)×0,6+С (1;12)×0,76+С (1;6)×0,8)=4,8/(3,6+9,12+4,8)=4,8/17,52~0,27
Автор ответа:
0
спасибо,но что то сомневаюсь в правильности, совсем непонятно что за формулу вы используете и откуда у вас 0,75? что такое (1;6) ? за что вы принимаете С? буду рада если вы поясните
Автор ответа:
0
поправил. должно быть 0,76 вместо 0,75. C (k;n)=n!/(k! (n-k)!)
Автор ответа:
0
ДУМАЕМ
ДВА события -
1- ВЫБРАТЬ любого студента - вероятность (Р1) рассчитаем по их количеству на факультете
2-он должен СДАТЬ экзамен - вероятность уже ДАНА (Р2)
Вероятность двух событий равна ПРОИЗВЕДЕНИЮ их вероятностей.
РЕШЕНИЕ
1) Выбрать студента - событие Р1
Всего студентов = 24. Р1эк= 12/24 = 0,5. Р1юр=Р1нал=0,25
Проверка на ПОЛНУЮ ВЕРОЯТНОСТЬ 0,5+0,25+0,25=1 - ПРАВИЛЬНО
2) Вероятность СДАТЬ (дана) - Р2эк=0,6. Р2юр=0,76, Р2нал=0,8
Вероятность ДВУХ событий - сумма произведений вероятностей
Рсдаст= Р1эк*Р2эк + Р1юр*Р2юр + Р1нал*Р2нал = 0,5*0,6+0,25*0,76+0,25*0,8=0,3+0,19+0,2 = 0,69 =69% - сдадут все студенты на факультете, а провалят -
Рпровал = 0,3+0,06+0,05=0,31=31%.
Проверяем на полную ВЕРОЯТНОСТЬ = 0,31+0,69=1-правильно
И вторая часть задачи - КТО сдаст экзамен - это по формуле Байеса.
Из 69% сдавших
Рэк = 0,3,/0,69 = 0,435=43,5% - ЭКОНОМИСТЫ
Рюр =0,19/0,69=0,275 = 27,5% -юрист.
Рнал=0,2/0,69=0,29 = 29% - налоговик
Проверяем на полную вероятность = 0,435+0,275+0,29=1 - правильно.
ОТВЕТ - вероятность что случайно выбранный студент будет ОДНОВРЕМЕННО и налоговиком и сдавшим экзамен =29%.
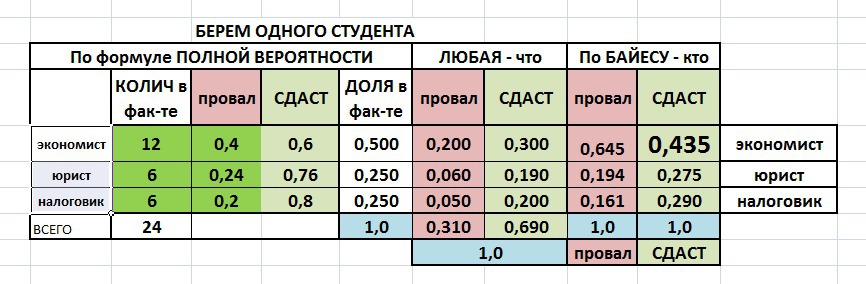
Прилагаю таблицу с расчетами
ДВА события -
1- ВЫБРАТЬ любого студента - вероятность (Р1) рассчитаем по их количеству на факультете
2-он должен СДАТЬ экзамен - вероятность уже ДАНА (Р2)
Вероятность двух событий равна ПРОИЗВЕДЕНИЮ их вероятностей.
РЕШЕНИЕ
1) Выбрать студента - событие Р1
Всего студентов = 24. Р1эк= 12/24 = 0,5. Р1юр=Р1нал=0,25
Проверка на ПОЛНУЮ ВЕРОЯТНОСТЬ 0,5+0,25+0,25=1 - ПРАВИЛЬНО
2) Вероятность СДАТЬ (дана) - Р2эк=0,6. Р2юр=0,76, Р2нал=0,8
Вероятность ДВУХ событий - сумма произведений вероятностей
Рсдаст= Р1эк*Р2эк + Р1юр*Р2юр + Р1нал*Р2нал = 0,5*0,6+0,25*0,76+0,25*0,8=0,3+0,19+0,2 = 0,69 =69% - сдадут все студенты на факультете, а провалят -
Рпровал = 0,3+0,06+0,05=0,31=31%.
Проверяем на полную ВЕРОЯТНОСТЬ = 0,31+0,69=1-правильно
И вторая часть задачи - КТО сдаст экзамен - это по формуле Байеса.
Из 69% сдавших
Рэк = 0,3,/0,69 = 0,435=43,5% - ЭКОНОМИСТЫ
Рюр =0,19/0,69=0,275 = 27,5% -юрист.
Рнал=0,2/0,69=0,29 = 29% - налоговик
Проверяем на полную вероятность = 0,435+0,275+0,29=1 - правильно.
ОТВЕТ - вероятность что случайно выбранный студент будет ОДНОВРЕМЕННО и налоговиком и сдавшим экзамен =29%.
Прилагаю таблицу с расчетами
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: norm66610
Предмет: Литература,
автор: zlatazavalova070
Предмет: Русский язык,
автор: weionh0w3n50hn
Предмет: Математика,
автор: ilya34rrus
Предмет: Алгебра,
автор: valya321