Предмет: Геометрия,
автор: sihgil
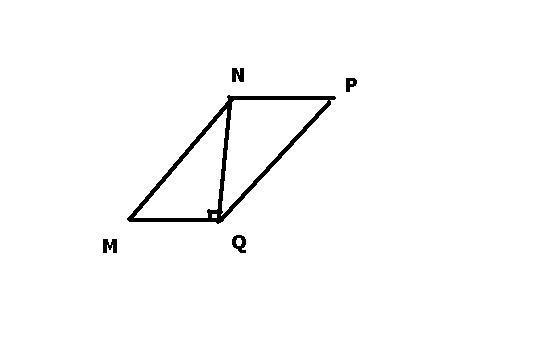
В параллелограмме MNPQ разность сторон MN и NP равна 2 см, а диагональ NQ является высотой параллелограмма. Найдите NQ, если периметр параллелограмма
равен 60 см.
Ответы
Автор ответа:
0
Известно, что MN-NP=2, примем MN=x, тогда NP=x-2, теперь подставим эти значения в формулу периметра параллелограма и найдём х:
2(х+(х-2))=60
4х-4=60
4х=64
х=16
MN=x=16 см⇒NP=16-2=14 см
По свойствам параллелограма противоположные стороны у него равны и ⇒NP=MQ
Рассмотрим ΔMNQ:
Известно, что NQ - высота паралелограма⇒∠MQN=90°⇒ΔMNQ - прямоугольный. По теореме Пифагора находим NQ:
NQ²=MN²-MQ²
NQ²=16²-14²
NQ²=256-196
NQ²=60
NQ=√60=2√15
Ответ: NQ= 2√15 см
2(х+(х-2))=60
4х-4=60
4х=64
х=16
MN=x=16 см⇒NP=16-2=14 см
По свойствам параллелограма противоположные стороны у него равны и ⇒NP=MQ
Рассмотрим ΔMNQ:
Известно, что NQ - высота паралелограма⇒∠MQN=90°⇒ΔMNQ - прямоугольный. По теореме Пифагора находим NQ:
NQ²=MN²-MQ²
NQ²=16²-14²
NQ²=256-196
NQ²=60
NQ=√60=2√15
Ответ: NQ= 2√15 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: hapshenkotetiana
Предмет: Биология,
автор: kostenkomasha136
Предмет: Литература,
автор: prostoroma57
Предмет: Математика,
автор: anas46611
Предмет: Химия,
автор: milankacom82