Question

Постройте график функции |x+2|-3/(x^2+4x-3|x+2|+4) и определите при каких значениях к график функции y=kx либо не пересекает этот график, либо имеет четное число общих точек с этим графиком. Заранее спасибо

Answer 1

$y= frac{|x+2|-3}{x^2+4x-3|x+2|+4}$

или

$y= frac{|x+2|-3}{(x^2+4x+4)-3|x+2|}$

или

$y= frac{|x+2|-3}{(x+2)^2-3|x+2|}$

или

$y= frac{|x+2|-3}{|x+2|(|x+2|-3)}$

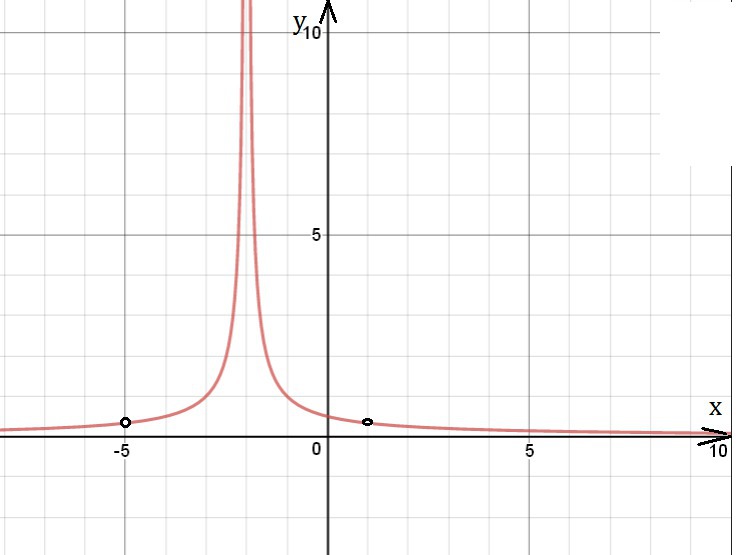
При  |x+2|-3≠0  график совпадает с графиком функции у =1/|x+2|

Находим значения при которых |x+2|-3=0   или   |x+2|=3
x+2=3      или   х+2=-3
х=1                   х=-5

Точки х=1 и х=-5 на графике отмечаем пустым кружком.
См. рисунок в приложении

Найдем, при каких k  х=-5 и х=1
k=-1/15  и k =1/3
прямая у=(1/3)х не имеет общих точек с графиком
и прямая у= (-1/15)х не имеет общих точек с графиком
при k=0 прямая у=кх имеет вид у=0 и тоже не имеет общих точек с графиком.
О т в е т.  При  k=-1/15; k=0; k=1/3  прямая у =кх не имеет общих точек с графиком.

Answer 2

так а чему равно k, там должно быть 3 значения

Answer 3

еще к равно 1

Answer 4

точнее -1