Question

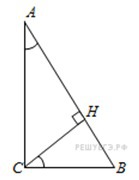
В треугольнике ABC угол C равен 90°,Bc=7 ,TgA=33/4√33 .Найдите высоту CH .

Answer 1

Тангенс угла А равен отношению противолежащего катета к прилежащему.  То есть TgA = BC/AC = 33/(4√33).  =>

AC = (7*4√33)/33 = 28√33/33.

По Пифагору: АВ = √(АС²+ВС²) = √(28²*33/33² +49*33/33) =√(2401/33). Или  АВ = 49/√33 = 49√33/33.

Высота из прямого угла треугольника к гипотенузе равна:

СН = АС*ВС/АВ (формула)  =>  

CН = (28√33*7*33)/(33*49√33) = 4 ед.

Ответ: СН = 4 ед.