Предмет: Геометрия,
автор: ALINAGREEN1312
Вписанная и описанная окружности. СРОЧНО ПОМОГИТЕ !!!Решить две задачи)
Приложения:
Ответы
Автор ответа:
0
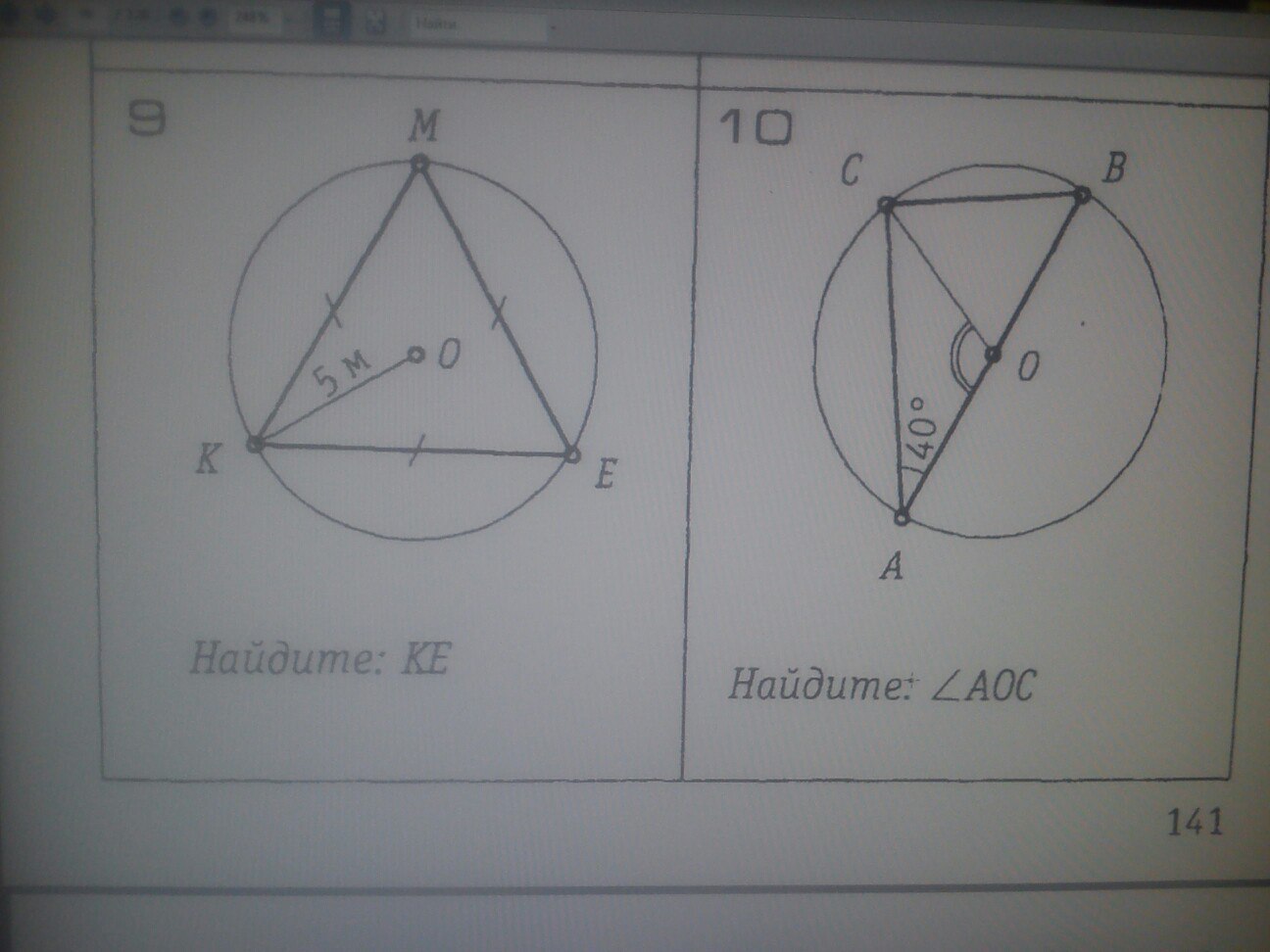
9)
Центр описанной около треугольника окружности-точка пересечения серединных перпендикуляров к его сторонам.
В равностороннем треугольнике точка пересечения высот, медиан, биссектрис совпадает.
Это означает, что центр описанной окружности лежит в точке пересечения медиан.
Медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины. Это означает, что радиус описанной окружности составляет 2/3 от длины медианы (она же высота). R=2h/3 (1);
Высоту найдём по теореме Пифагора: h^2=a^2-(a/2)^2;
h^2=3a^2/4;
h=a√3/2;
подставим в(1):
R=2a√3/2*3=а√3/3;
a=3R/√3=3R*√3/√3*√3=R√3;
по условию R=5;
a=5√3
ответ: 5√3
10) треугольник АОС равнобедренный: ОС и ОА радиусы; углы А и С равны по 40°.
угол АОС=180-(40+40)=100°;
ответ: 100
Похожие вопросы
Предмет: Английский язык,
автор: wearvs
Предмет: Алгебра,
автор: Marinka0987654321
Предмет: Русский язык,
автор: xakkerist
Предмет: Алгебра,
автор: wwwdaniru
Предмет: Химия,
автор: Mary1998123