Question

Постройте график функции:
$1) y = |sinx| + sinx \ \ 2) y = frac{sin(|x| + x)}{cos|x|}$

Answer 1

1) Раскроем модуль. Тогда функция будет задана так:
$y= left { {{2sinx, 2 pi n leq x leq pi +2 pi n} atop {0, pi +2 pi n textless x textless 2 pi+2 pi n}} right.$, где n∈Z.
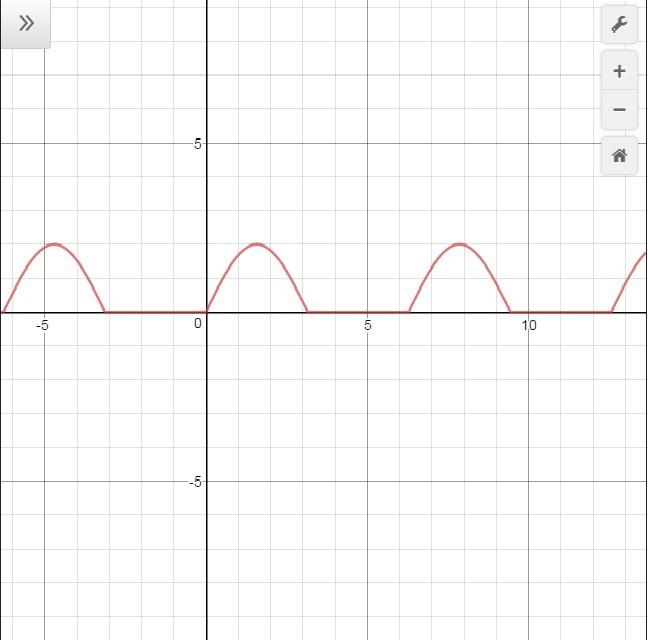
Сначала строим график функции 2sinx на отрезке 0 до π. Для этого нужно график функции sinx на этом отрезке растянуть в два раза вдоль оси OY. 
Теперь на промежутке от π до 2π проводим прямую совпадающую с осью OX. Дальше построенный кусок графика повторяется каждые 2π. График приложен к ответу.
2. Опять же раскрываем модуль. Пусть x≥0, тогда для $x neq frac{ pi }{2} + pi n$:
$y= frac{sin2x}{cosx} =frac{2sinxcosx}{cosx}=2sinx$
Если же x<0, то опять же для $x neq frac{ pi }{2} + pi n$:
$y= frac{0}{cos(-x)} =0$
Строим сначала опять график функции 2sinx для x≥0, выкалывая точки, которые не входят в область определения.
Для x<0 график совпадает с осью ОХ, на которой выколоты точки $frac{ pi }{2} + pi n$
Графики к ответу приложены. Но точки, о которых говорилось выше придется выколоть самостоятельно. Уж больно кривой сервис для построения попался.