Предмет: Алгебра,
автор: Kotovsky54
Помогите решить неравенство (смотри фото)
Приложения:
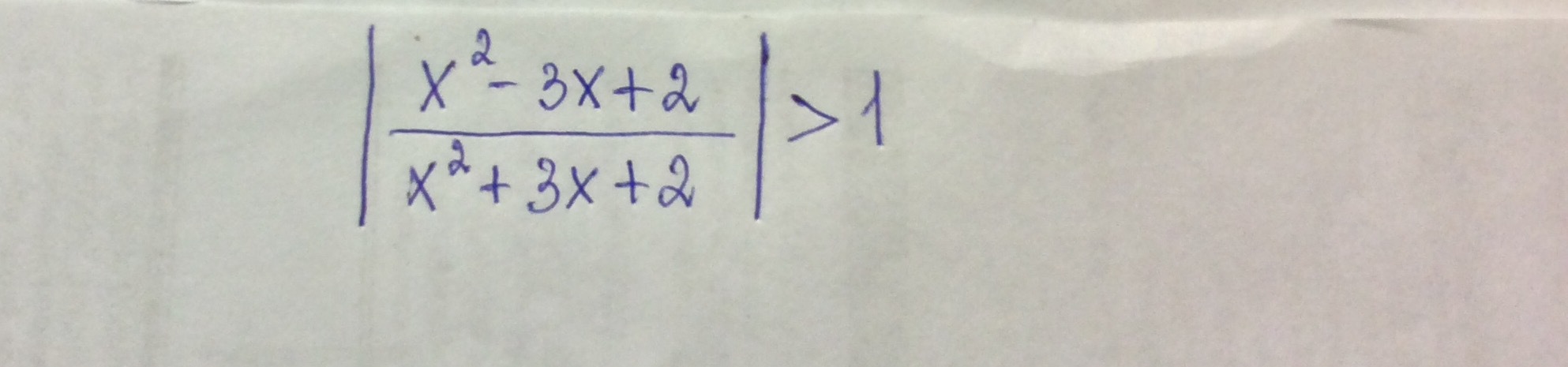
Ответы
Автор ответа:
0
Обе части неотрицательны, поэтому че бы не возвести их в квадрат? Возведем и преобразуем:
![|frac{x^2-3x+2}{x^2+3x+2}| textgreater 1 \
(frac{x^2-3x+2}{x^2+3x+2})^2-1 textgreater 0 \
(frac{x^2-3x+2}{x^2+3x+2}+1)(frac{x^2-3x+2}{x^2+3x+2}-1) textgreater 0 \
(frac{x^2-3x+2+x^2+3x+2}{x^2+3x+2})(frac{x^2-3x+2-x^2-3x-2}{x^2+3x+2}) textgreater 0 \
(frac{2x^2+4}{x^2+3x+2})(frac{-6x}{x^2+3x+2}) textgreater 0 \
frac{12x(x^2+2)}{(x^2+3x+2)^2} textless 0 \
left { {{x neq -2, x neq -1} atop {12x textless 0}} right.](https://tex.z-dn.net/?f=+%7Cfrac%7Bx%5E2-3x%2B2%7D%7Bx%5E2%2B3x%2B2%7D%7C+textgreater++1+%5C+%0A%28frac%7Bx%5E2-3x%2B2%7D%7Bx%5E2%2B3x%2B2%7D%29%5E2-1+textgreater++0+%5C+%0A%28frac%7Bx%5E2-3x%2B2%7D%7Bx%5E2%2B3x%2B2%7D%2B1%29%28frac%7Bx%5E2-3x%2B2%7D%7Bx%5E2%2B3x%2B2%7D-1%29+textgreater++0+%5C+%0A%28frac%7Bx%5E2-3x%2B2%2Bx%5E2%2B3x%2B2%7D%7Bx%5E2%2B3x%2B2%7D%29%28frac%7Bx%5E2-3x%2B2-x%5E2-3x-2%7D%7Bx%5E2%2B3x%2B2%7D%29+textgreater++0+%5C+%0A%28frac%7B2x%5E2%2B4%7D%7Bx%5E2%2B3x%2B2%7D%29%28frac%7B-6x%7D%7Bx%5E2%2B3x%2B2%7D%29+textgreater++0+%5C+%0Afrac%7B12x%28x%5E2%2B2%29%7D%7B%28x%5E2%2B3x%2B2%29%5E2%7D+textless++0+%5C+%0A+left+%7B+%7B%7Bx++neq+-2%2C+x+neq+-1%7D+atop+%7B12x+textless++0%7D%7D+right.+%0A "|frac{x^2-3x+2}{x^2+3x+2}| textgreater 1 \
(frac{x^2-3x+2}{x^2+3x+2})^2-1 textgreater 0 \
(frac{x^2-3x+2}{x^2+3x+2}+1)(frac{x^2-3x+2}{x^2+3x+2}-1) textgreater 0 \
(frac{x^2-3x+2+x^2+3x+2}{x^2+3x+2})(frac{x^2-3x+2-x^2-3x-2}{x^2+3x+2}) textgreater 0 \
(frac{2x^2+4}{x^2+3x+2})(frac{-6x}{x^2+3x+2}) textgreater 0 \
frac{12x(x^2+2)}{(x^2+3x+2)^2} textless 0 \
left { {{x neq -2, x neq -1} atop {12x textless 0}} right.")
Вот и ответ x∈(-oo; -2)∪(-2; -1)∪(-1; 0)
Вот и ответ x∈(-oo; -2)∪(-2; -1)∪(-1; 0)
Похожие вопросы
Предмет: Физика,
автор: picoo
Предмет: Алгебра,
автор: borisovnazlata
Предмет: Английский язык,
автор: kirilldemon6
Предмет: Алгебра,
автор: TenraN