Question

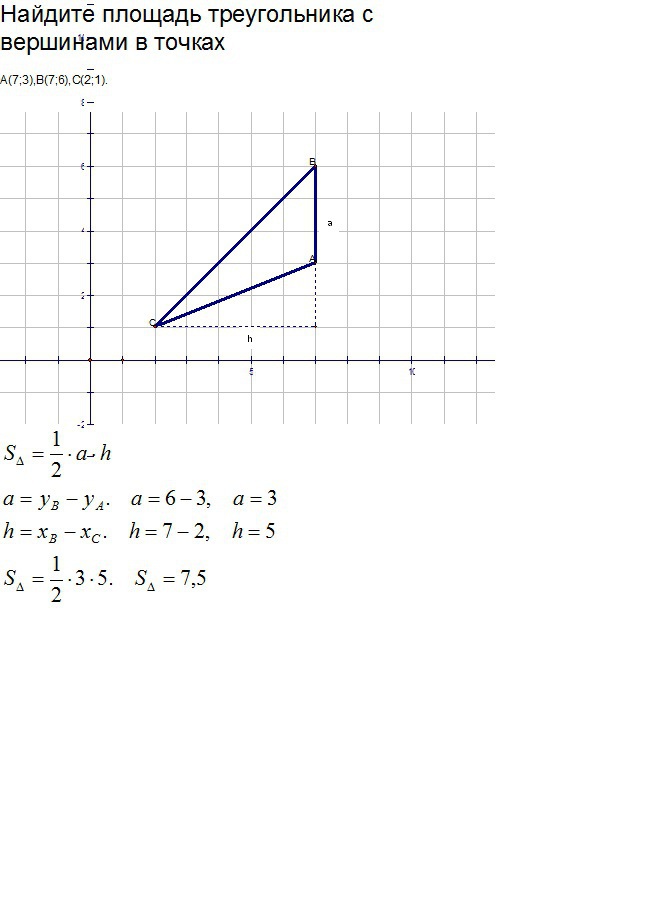
Найдите площадь треугольника с вершинами в точках
А(7;3),В(7;6),С(2;1).

Answer 1

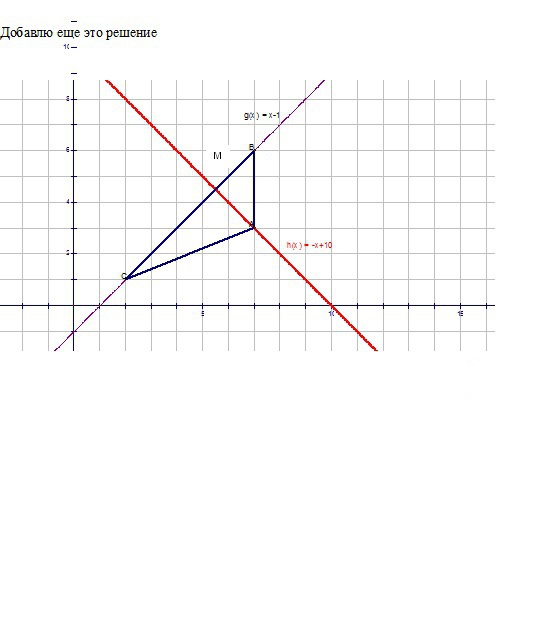
Найдём уравнение прямой, описывающей лини. BC (основание треугольника)  y(x)=5*x/5-1 (здесь 5 в числителе - это расстояние между вертикальными координатами точек B и C, а 5 в знаменателе - расстояние между их горизонтальными координатами ). Общее уравнение прямой запишем как 1*y-1*x+1=0. Теперь расстояние между точкой А и прямой BC (высота треугольника) равна d=|-1*7+1*3+1|/√(1²+1²)=3/√2=2,121. Длина стороны ВС равна L=√(5²+5²)=√50=7,071. Теперь площадь треугольника ищем как полупроизведение основания ВС на высоту d, то есть S=0,5*7,071*2,121=7,5 единиц.

Answer 2

решение во вложении-------------------