Предмет: Математика,
автор: isaidova
Ответы
Автор ответа:
0
Решения на фото. Некоторые объяснения ниже.
№1
Обычные действия с дробями. Приводим к общему знаменателю (х+1)(х-1). Раскрываем скобки. Используем формулы сокращенного умножения.
№2
Выполняем замену. Решаем квадратное уравнение и находим корни. Затем производим обратную замену и находим х.
№3
Данный пример можно решить методом интервалов.
Дробь а/b>0, если a>0, b>0 или a<0, b<0. Произведение ab>0 имеет тоже решение, значит мы можем заменить дробь произведением. Аналогичное решение и со знаком <.
Дробь a/b≥0. Дробь равна нулю только если числитель равен нулю. Произведение же равно нулю, если a или b равно нулю. В этом случае нам нужно учесть ОДЗ: знаменатель b≠0
ab>0⇔a·b>0,
ab≥0⇔
№4
Относительность движения, а также формулы расстояния S, скорости v и времени t движения.При движении по течению скорости складываем, против - вычитаем (из собственной скорость реки).
Выйти на решение можно через время движения. Что такое время? Это S/v. Запишем это отношение для движения по течению и против. Затем в условие задачи подставляем полученные t. Минуты надо обязательно перевести в часы, чтобы единицы измерения соответствовали друг другу.
Далее, приводим к общему знаменателю. S переносим в левую часть. т.к. нам нужно оставить с права только скорости. Мы получили уравнение скоростей движения по течению и против.
Теперь и
и  можно заменить суммой и разностью скоростей собственной и реки соответственно. Решаем получившееся уравнение и выводи
можно заменить суммой и разностью скоростей собственной и реки соответственно. Решаем получившееся уравнение и выводи  . Все данные у нас есть.
. Все данные у нас есть.
№5
У Мордковича есть хороший учебник 10-11 класса, в котором разъяснено как решать уравнения с параметрами.
Здесь же у нас линейное уравнение, котрое быстро решается. Главное не забыть про область допустимых значений!
№6
Довольно сложная задача и за два дня так и не нашла решения((((
№1
Обычные действия с дробями. Приводим к общему знаменателю (х+1)(х-1). Раскрываем скобки. Используем формулы сокращенного умножения.
№2
Выполняем замену. Решаем квадратное уравнение и находим корни. Затем производим обратную замену и находим х.
№3
Данный пример можно решить методом интервалов.
Дробь а/b>0, если a>0, b>0 или a<0, b<0. Произведение ab>0 имеет тоже решение, значит мы можем заменить дробь произведением. Аналогичное решение и со знаком <.
Дробь a/b≥0. Дробь равна нулю только если числитель равен нулю. Произведение же равно нулю, если a или b равно нулю. В этом случае нам нужно учесть ОДЗ: знаменатель b≠0
ab>0⇔a·b>0,
ab≥0⇔
№4
Относительность движения, а также формулы расстояния S, скорости v и времени t движения.При движении по течению скорости складываем, против - вычитаем (из собственной скорость реки).
Выйти на решение можно через время движения. Что такое время? Это S/v. Запишем это отношение для движения по течению и против. Затем в условие задачи подставляем полученные t. Минуты надо обязательно перевести в часы, чтобы единицы измерения соответствовали друг другу.
Далее, приводим к общему знаменателю. S переносим в левую часть. т.к. нам нужно оставить с права только скорости. Мы получили уравнение скоростей движения по течению и против.
Теперь
№5
У Мордковича есть хороший учебник 10-11 класса, в котором разъяснено как решать уравнения с параметрами.
Здесь же у нас линейное уравнение, котрое быстро решается. Главное не забыть про область допустимых значений!
№6
Довольно сложная задача и за два дня так и не нашла решения((((
Приложения:
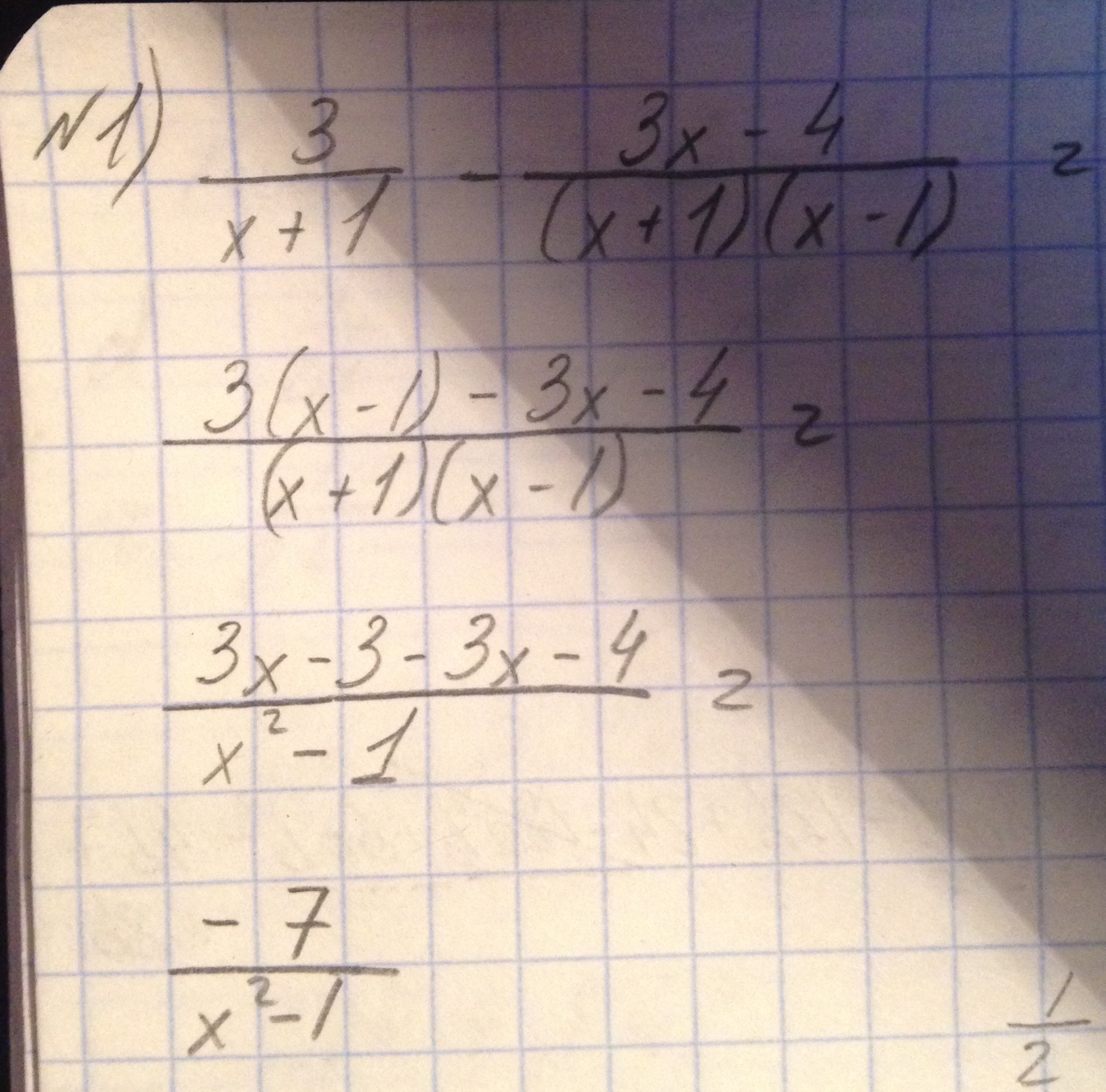
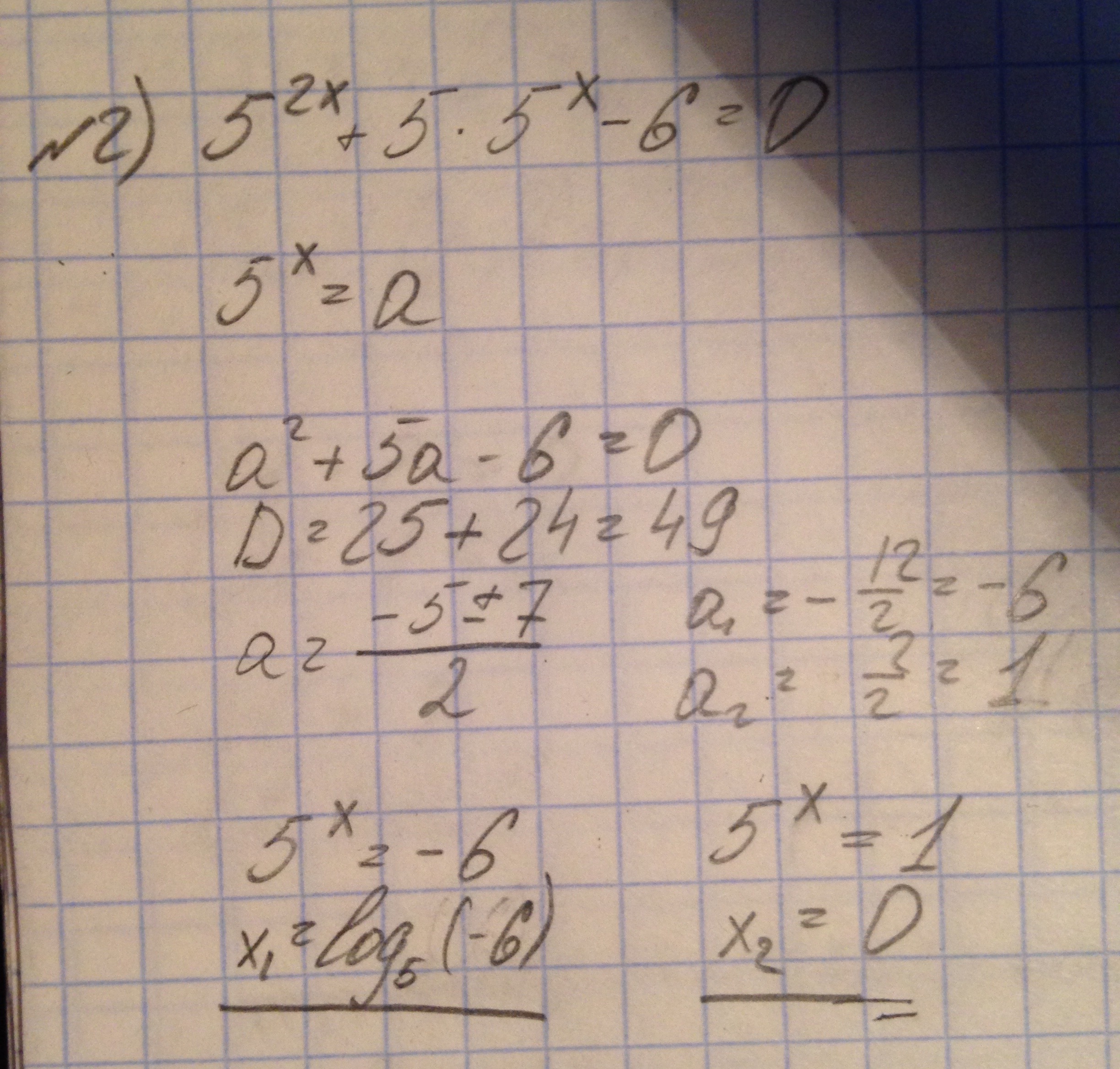
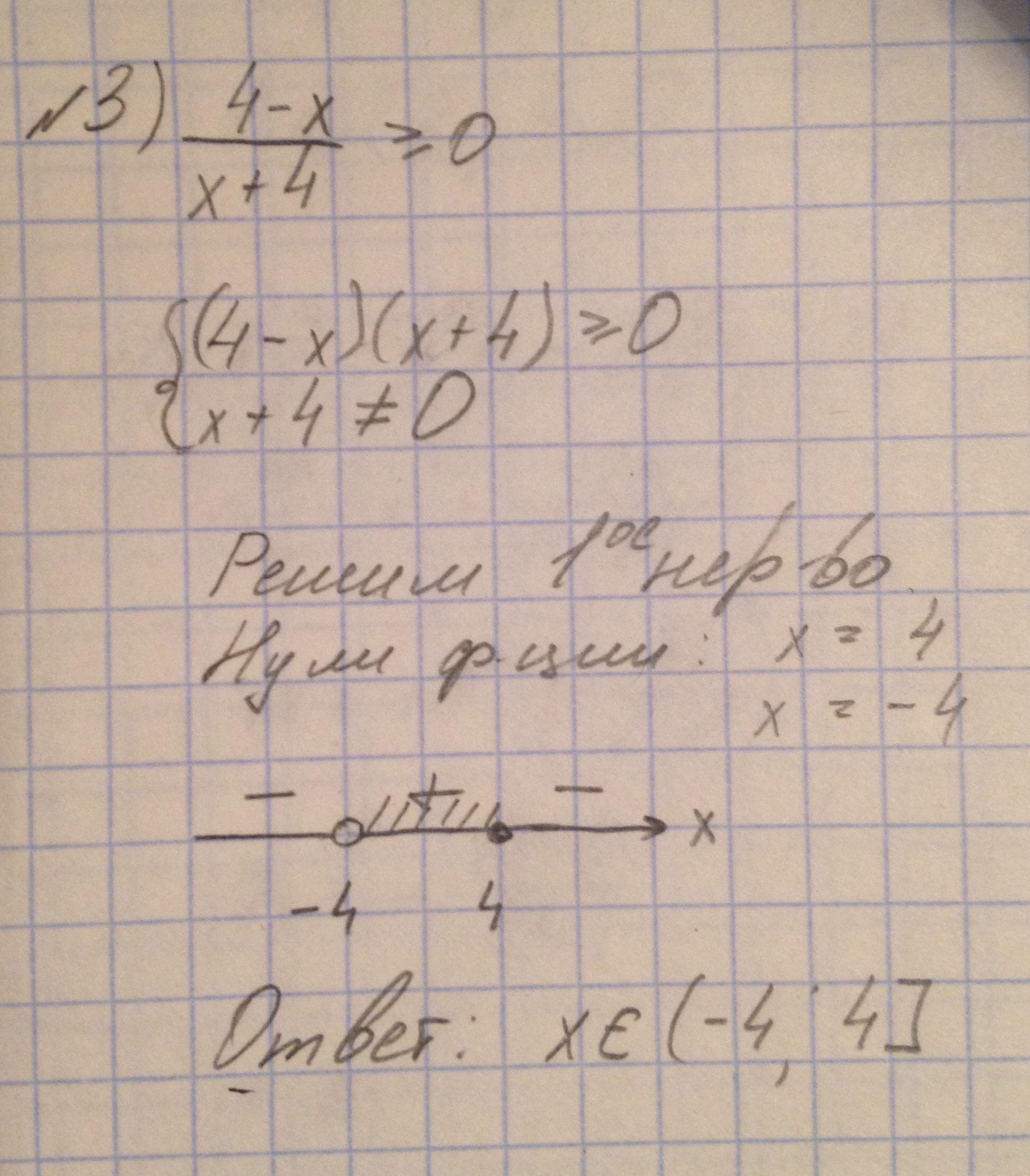


Автор ответа:
0
Спасибо Большущее
Похожие вопросы
Предмет: Математика,
автор: andrianartem503
Предмет: Английский язык,
автор: viktoria11chuk11
Предмет: Русский язык,
автор: Zaitcevan65
Предмет: Физика,
автор: antonminkin
Предмет: Математика,
автор: Zaliya669