Question

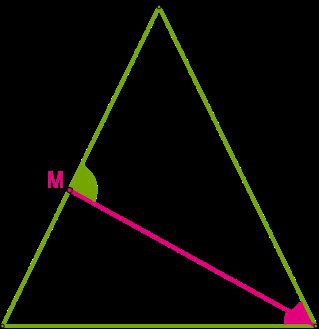
В равнобедренном треугольнике NLT проведена биссектриса TM угла T у основания NT,
∡TML=72°. Определи величины углов данного треугольника (если это необходимо, округли ответ до тысячных).

∡N=
°

∡T=
°

∡L=
°

Answer 1

В тр-ке NMT ∠ТNM+∠NTM=∠TML=72° (Величина смежного угла тр-ка равна сумме двух других его внутренних углов).
Пусть ∠LNТ=∠LТN=x, тогда ∠NTM=x/2,
x+x/2=72,
1.5x=72°,
x=48°.
В тр-ке NLТ ∠N=∠T=48°.
∠L=180-∠N-∠T=180-2·48=84°.