Question

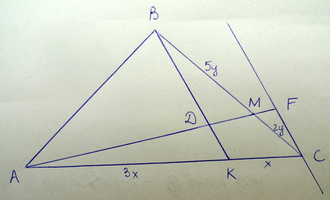
В треугольнике АВС точка К лежит на стороне АС и делит её в отношении СК : КА = 1 : 3; точка М лежит на стороне ВС и делит её в отношении СМ : МВ = 2 : 5; . D – точка пересечения отрезков АМ и ВК. В каком отношении точка D делит отрезок АМ?

Answer 1

Проведём прямую AM.
Проведём прямую FC ║ BK.

ΔDBM ~ ΔCFM (по двум углам).
Тогда: DM / MF = BM / CM = 5/2 ⇒ DF = 7/5·DM

В ΔCAF, согласно теореме Фалеса: AD / DF = AK / KC = 3 ⇒ AD = 3·DF =
= 3· 7/5·DM = 21/5·DM

AD / DM = 21/5