Предмет: Алгебра,
автор: ATGC
Решите плз. С подробным решениям
Приложения:
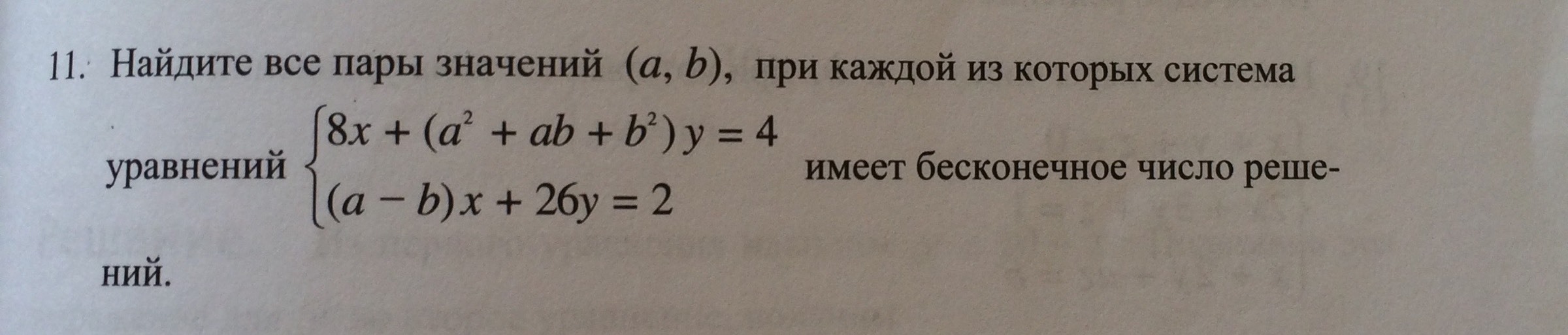
Ответы
Автор ответа:
0
графиками этих уравнений являются прямые.Чтобы две прямые имели бесконечное множество решений, они должны СОВПАДАТЬ, то есть верхнее и нижнее уравнения -это одно и то же уравнение.
P.S: чтобы увидеть что написано дальше, надо зайти с компьютера или смотри скрин

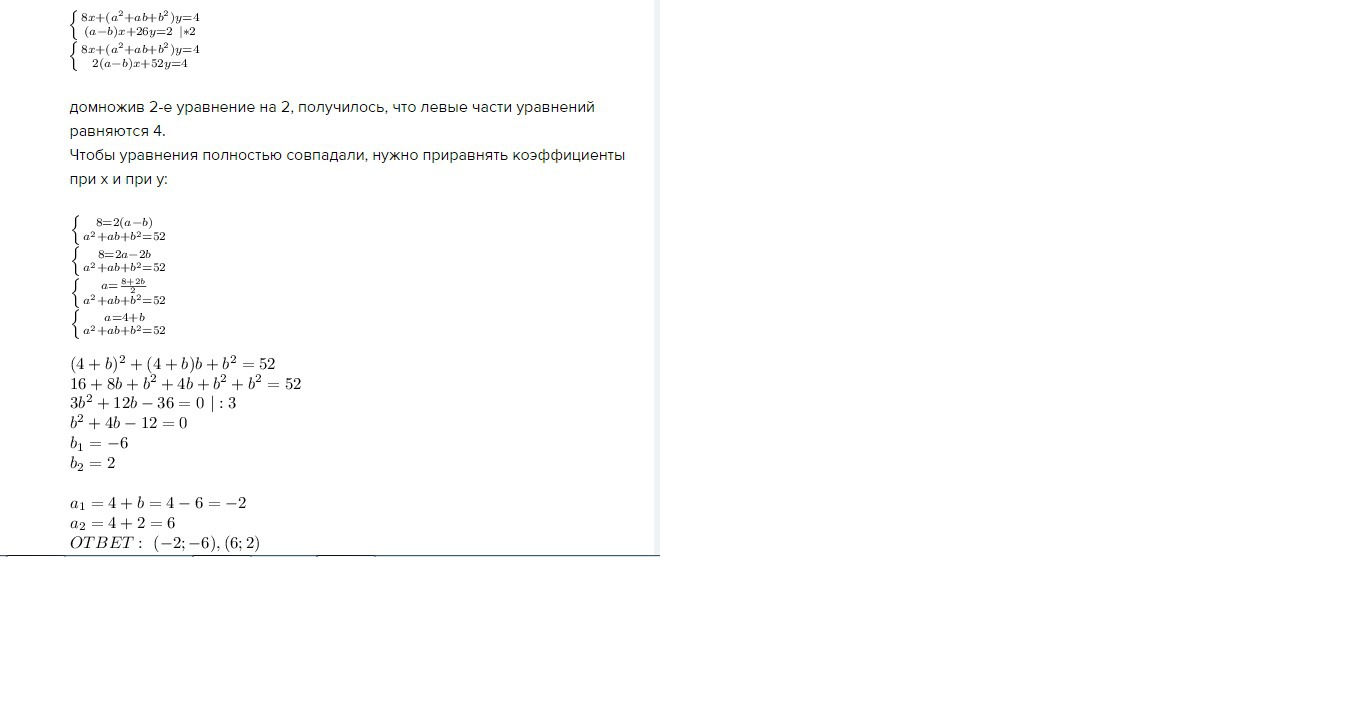
домножив 2-е уравнение на 2, получилось, что левые части уравнений равняются 4.
Чтобы уравнения полностью совпадали, нужно приравнять коэффициенты при х и при у:

P.S: чтобы увидеть что написано дальше, надо зайти с компьютера или смотри скрин
домножив 2-е уравнение на 2, получилось, что левые части уравнений равняются 4.
Чтобы уравнения полностью совпадали, нужно приравнять коэффициенты при х и при у:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: haaaauuuu
Предмет: Биология,
автор: Godzilla2
Предмет: Українська мова,
автор: Rikardo238
Предмет: География,
автор: pivenanna2001
Предмет: Литература,
автор: AliceEatingCakes