Question

Окружность, вписанная в прямоугольный треугольник ABC (где угол  С = 90) касается катета ВС в точке Н, биссектриса угла А пересекает катет ВС в точке М. Найти НМ, если СН = 4, ВН = 12

Answer 1

Решение в скане.................

Answer 2

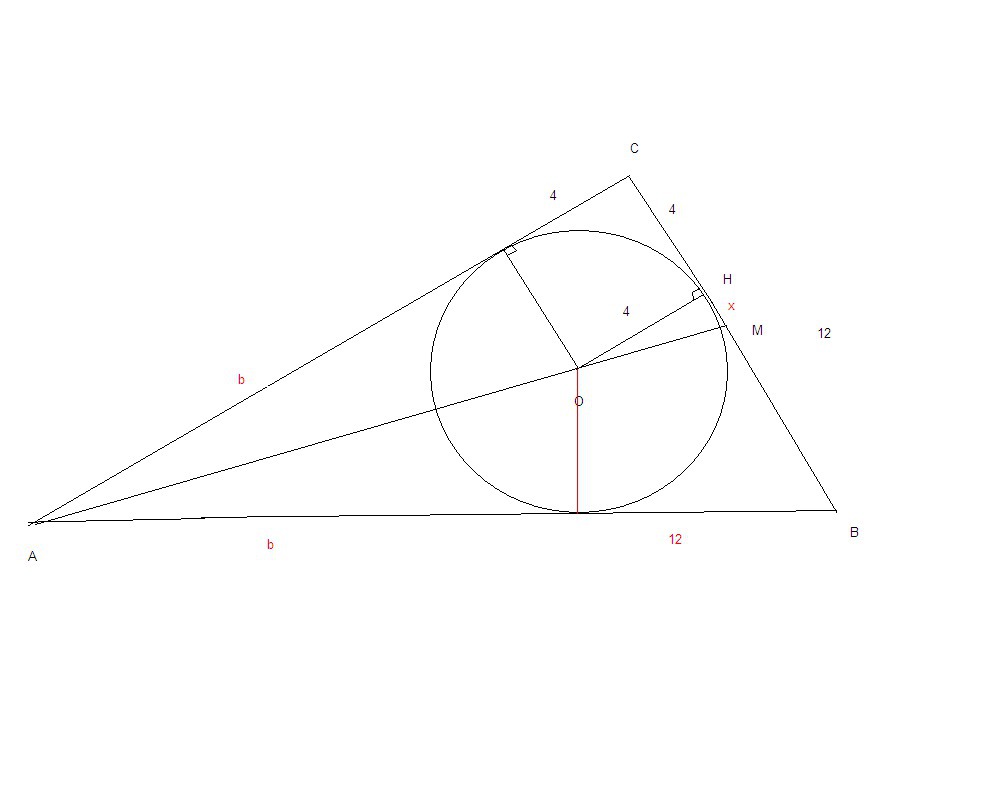
смотри рисунок.
сделаем очевидные обозначения и неизвестные.
треуг. ОНМ и АСМ подобны
из них    ОН/НМ=АС/СМ    т.е.  4/х=(в+4)/(4+х)
а из ΔАВС      (в+4)²+16²=(в+12)²  отсюда  в=8
подставляем  в и находим  х.
х=2