Question

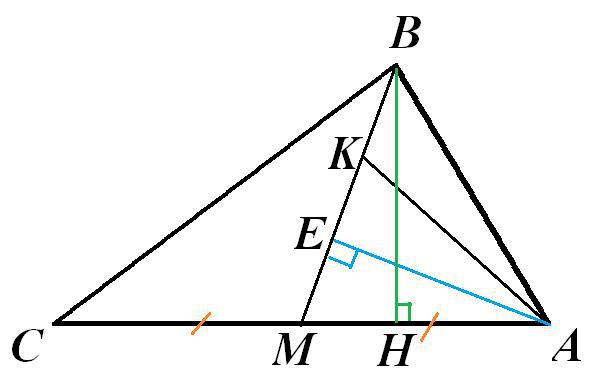
В треугольнике ABC на медиане ВМ взято точку К так, что ВК:КМ=1:2.Найдите отношение площади треугольников АВК и АВС.

Answer 1

Медиана ВМ делит Δ АВС на два равновеликих треугольника, т.е. два треугольника с равными площадями ⇒ $S_{ABC}= 2S_{ABM}$.
Из равенства ВК:КМ=1:2 следует, что МК=2КВ или $KB= frac{1}{3}MB$.
Пусть АЕ - высота в Δ АВМ. Тогда АЕ также и высота в Δ АМК, и в Δ АВК.
Распишем площади треугольников:
$S_{ABM}= frac{1}{2}AE*BM;\ S_{ABK}= frac{1}{2}AE*BK=frac{1}{2}AE*frac{1}{3}BM=frac{1}{6}AE*BM.$
Отсюда видно, что $S_{ABK}= frac{1}{3} S_{ABM}$
Тогда интересующее нас отношение равно:
$dfrac{S_{ABK}}{S_{ABC}} = dfrac{frac{1}{3} S_{ABM}}{2S_{ABM}} = dfrac{1}{6}$
Ответ: 1:6.