Предмет: Математика,
автор: Крис201611
Вычислите sin в данном выражении
Приложения:
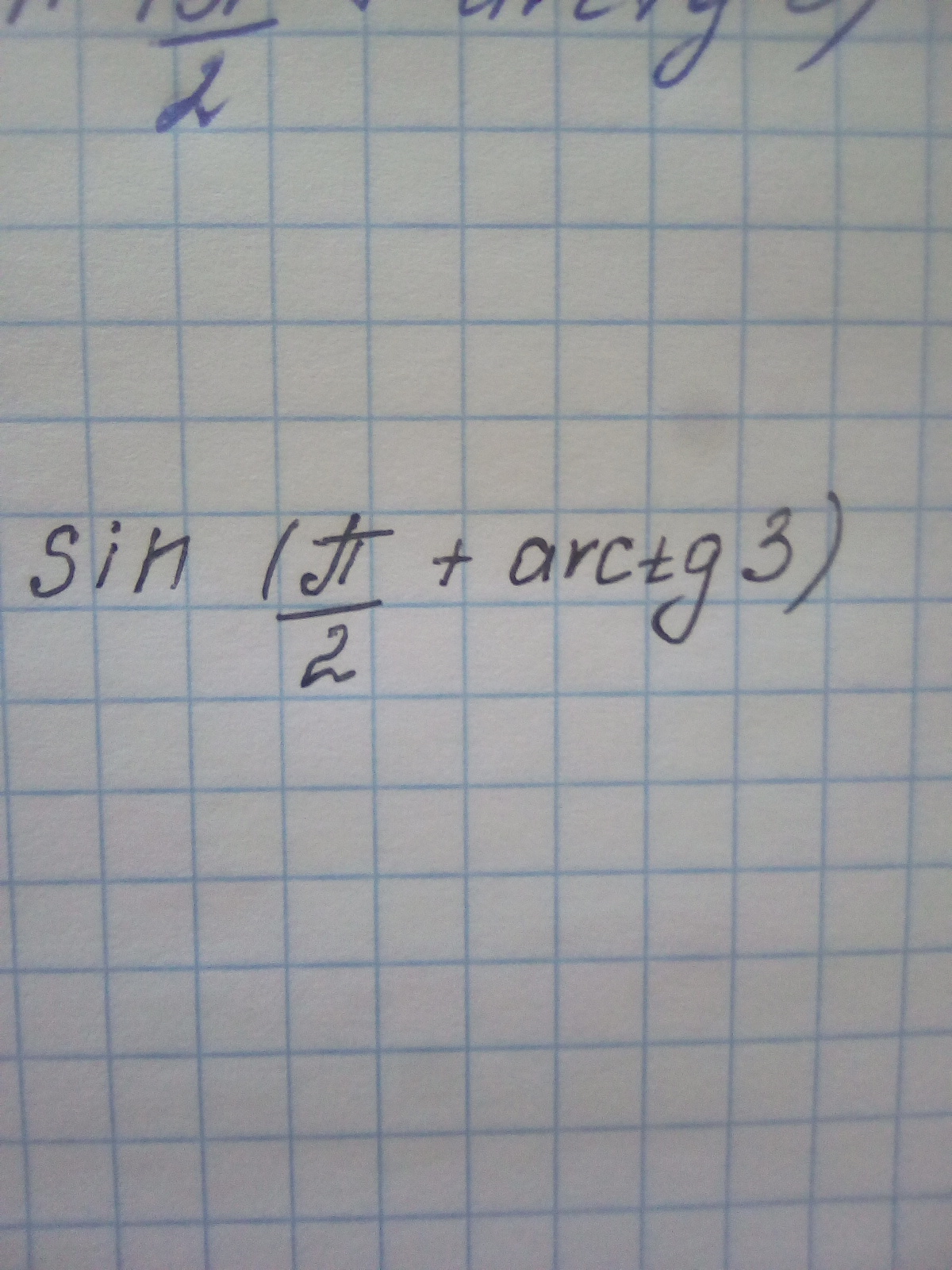
Ответы
Автор ответа:
0
Расписать как cos(arctg3)
Пусть arctg3 = t, где -п/2 < t < п/2,
Тогда требуется найти значение выражения cos(arctg3) = cos t.
Из равенства arctg3 = t следует обратное: tg t = 3. Учитывая положительность тангенса (он равен 3) и неравенство -п/2 < t < п/2, заключаем, что t - угол 1-й четверти, где все тригон.величины положительны.
Итак, задача - найти cos t при данном tg t = 3.
1+tg^2t=1/(cos^2t)
cos^2t=1/(1+tg^2t)=1/(1+(3)^2)=1/10
cost=+-sqrt(1/10)=+-(sqrt(10))/10
Учитывая, доказанную выше положительность косинуса, получаем, что и
sin(pi/2+arctg3)=cos(arctg3)=(sqrt(10)/10)
Ответ: (sqrt(10)/10)
Пусть arctg3 = t, где -п/2 < t < п/2,
Тогда требуется найти значение выражения cos(arctg3) = cos t.
Из равенства arctg3 = t следует обратное: tg t = 3. Учитывая положительность тангенса (он равен 3) и неравенство -п/2 < t < п/2, заключаем, что t - угол 1-й четверти, где все тригон.величины положительны.
Итак, задача - найти cos t при данном tg t = 3.
1+tg^2t=1/(cos^2t)
cos^2t=1/(1+tg^2t)=1/(1+(3)^2)=1/10
cost=+-sqrt(1/10)=+-(sqrt(10))/10
Учитывая, доказанную выше положительность косинуса, получаем, что и
sin(pi/2+arctg3)=cos(arctg3)=(sqrt(10)/10)
Ответ: (sqrt(10)/10)
Похожие вопросы
Предмет: Английский язык,
автор: ghhhhrt
Предмет: Математика,
автор: radjapovaodina
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: мариякукарача