Question

Две касающиеся внешним образом в точке К окружности, радиусы которых равны 40 и 42, касаются сторон угла с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС.

Answer 1

решение в скане.      Нудновато доказывал то, что ВС делится пополам. Да и радиус кажется большим. И если бы ставил сразу численные решения буковок меньше надо бы писать.

Answer 2

То, что ВС делится пополам- очевидно из св-в касательных.
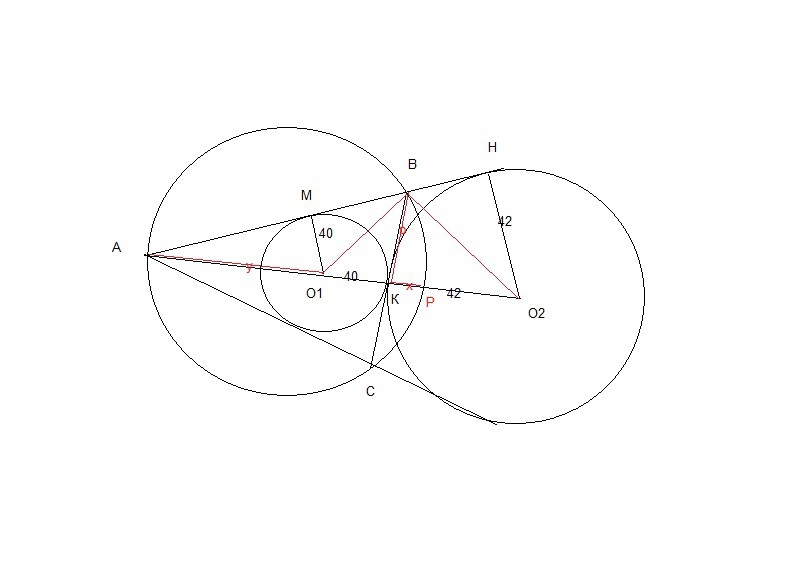
Ну да ладно. Сделаем обозначения известного (черным) и неизвестного и допостроения (красным).
Опять же из касательных треугольник О1ВО2 - прямоугольный с высотой  р.
из подобных прямоуг. треуг. АО1М и АО2Н -    у/40=(у+40+42)/42
   у=1640

из треуг. О1ВО2    р²=40*42

из треуг. АВР   (АР- диаметр , значит и гипотенуза)  
  р²= (у+40)*х  подставляем у=1640
р²=1680*х        приравниваем правые части

1680*х=40*42
х=1
тогда диаметр = 1680+1=1681
а радиус =1681/2=840.5