Question

К гипотенузе прямоугольного треугольника проведена биссектриса, которая разбивает
ее на отрезки длиной 1 и 3. Найдите площадь этого треугольника.

Answer 1

Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
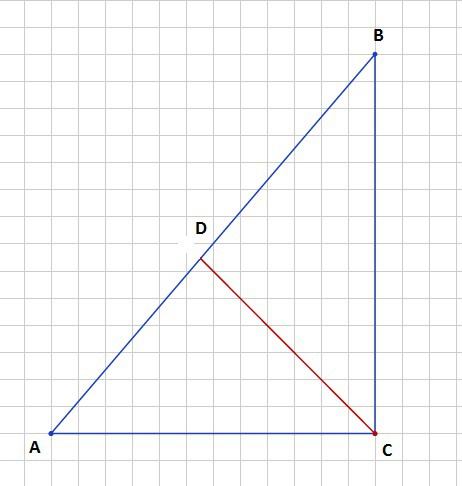
Обозначим заданный треугольник как АВС и биссектрису CD, а AD=1, DB=3.
AD/DB=AC/BC=1/3 ⇒ BC=3AC
Гипотенуза АВ по теореме Пифагора равна
АВ²=AC²+BC²
По условию АВ=АD+DB=1+3=4, значит можно записать
4²=AC²+BC²
Подставляем вместо ВС
AC²+(3AC)²=4²
AC²+9AC²=16
10AC²=16
AC²=1,6
AC=√1,6
BC=3√1,6
Площадь прямоугольного треугольника
S=AC*BC/2=(√1,6*3√1,6)/2=4,8/2=2,4 ед²

Ответ: 2,4 ед²