Question

ПОМОГИИИИИИИИИТЕ .Треугольник АВС. АВ=3см, ВС=8см. Может ли S=15см^2? С пояснением, пожалуйста

Answer 1

Вспоминаем формулу Герона для площади треугольника.
S=√[p(p-a)(p-b)(p-c)]  (1)
p - это полупериметр.
Пусть a=3, b=8, тогда p=(3+8+c)/2=1/2×(с+11)
Подставляя выражение для p в (1) получим:
√[1/2×(с+11)×(1/2×(с+11)-3)×(1/2×(с+11)-8)×(1/2×(с+11)-с)]=15
Возводим обе части уравнения в квадрат
1/2×(с+11)×(1/2×(с+11)-3)×(1/2×(с+11)-8)×(1/2×(с+11)-с)=225
1/2×(с+11)х1/2×(с+11-6)×1/2×(с+11-16)×1/2×(с+11-2с)=225
1/16×(с+11)(с+5)(с-5)(11-с)=225
(11+с)(11-с)(с+5)(с-5)=225×16
(121-с²)(с²-25)=225×16
121с²-25×121-с⁴+25с²=225×16
с⁴-146с²+121×25+225×16=0
с⁴-146с²+6625=0
Полагаем с²=х, тогда х²-146х+6625=0
D=146²-4×6625=-5188 < 0
Уравнение не имеет действительных корней, поэтому с также не является действительным числом, следовательно, такой треугольник не может существовать.

Ответ: Не может.

Answer 2

Вариант решения. 

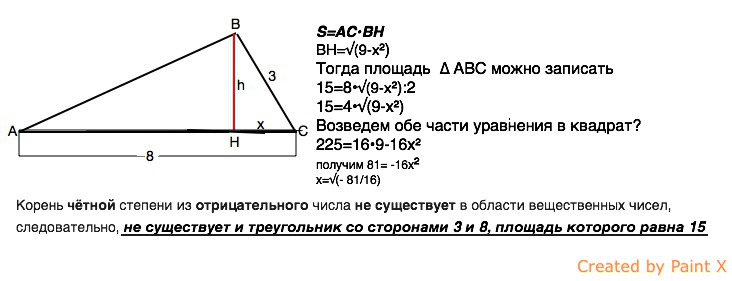
Обозначим  высоту АН, отрезок НВ=х

Выразим высоту из прямоугольного  ∆ АВН

АН=√(9-х²)

Тогда площадь  ∆ АВС можно записать 

15=8•√(9-х²):2

15=4•√(9-х²)

Возведем обе части уравнения в квадрат.

225=16•9-16x² 

получим 81= -16х² 

х=√(- 81/16)

Корень чётной степени из отрицательного числа не существует в области вещественных чисел, следовательно, 

не существует треугольник со сторонами 3 и 8, площадь которого равна 15 см²